Vessel with liquids having different refractive index

[sylwesh98]

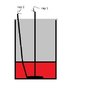
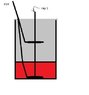
1.Problem: A vessel is quarter filled with a liquid of refractive index A. the remaining parts of the vessel is filled with an immiscible liquid of refractive index 3A/2. The apparent depth of the vessel is 50% of the actual depth. the value of A is?
1)1 2)3/2 3)2/3 4)4/3

Solution: 1

Method I've tried: I really don't know how to solve this problem! i know if there is only one liquid. but there are two liquids so iam little confused.

 

[lightgrav]

did you draw a ray diagram?
Ray 1 from "coin" at vessel bottom center, straight along the Normal all the way into air.
Ray 2 from coin is tilted at angle θ_bottom in the index bottom, refracting to angle θ_top in index top, refracting to angle θ_air in air.
"virtual ray 2" traces back straight along Ray 2 in air, but does not refract at either surface.

 

[sylwesh98]

ray is not clear i don't get it! is it the ray?

 

[proton007007]

ray is not clear i don't get it! is it the ray?

That is the ray 1 and its correct . Make one more ray .

 

[DEvens]

What you need to do is this:
- Trace a ray from the coin to the top. But have it at some angle so that it will refract at each boundary.
- Follow the ray all the way from the coin to the top. And project this ray to an observer. Don't forget to do this as a function of the value of A.
- Trace another ray straight up. (You have that.)
- Now you have a vertical, and an apparent angle at the observer.
- Work out from this where the coin looks like it is sitting, but do it as a function of the value A.
- Now you were told where the coin looks like it is sitting.

 

[sylwesh98]

but does it have something to do with the liquid with 2 different refractive media, and i can't trace another ray! its a little bit confusing!

 

[sylwesh98]

please can anyone provide me with a rough ray diagram so that i can proceed?!

 

[DEvens]

please can anyone provide me with a rough ray diagram so that i can proceed?!

I will need to see you make some effort before I will help you more. I think I have given you plenty to solve the problem if you will just make the effort.

Review your notes on what happens when light passes from a medium with one refractive index to a medium with a different refractive index. Look for Snell's law.

 

[sylwesh98]

is this one correct?

 

[DEvens]

Ok, making some progress.

So, now, what formula applies at each interface? When a ray moves from a higher index media to a lower index media, does it get closer to the normal or farther away? And by how much? Don't forget that you have two places where the ray changes material.

To figure out the apparent depth of the tank you will need to be comparing to a situation with no fluid in the way that produces the same situation for an observer. So when you figure out where the rays are above the tank you will want to be projecting them back as though the liquid was not there, and see where it makes it look like the object at the bottom of the tank is.

 

[sylwesh98]

when the ray 2 leaves the medium one it will refract towards normal as it is passing from rarer to denser medium, after that from medium 2 to air it will be passing away for the normal as it is passing from denser to rared medium from that ray when it is seen from the eye it appears that the ray is coming from the middle of the vessel. but how can we solve if there are 2 liquids.

 

[DEvens]

Nearly there.

What formula applies at each interface? Write down Snell's law. You have a formula that relates the index of refraction at the red-to-grey interface. And now you can write down some formulas that give you the apparent depth as a function of the index of refraction. And you know the depths. And you know how deep the coin appears to be. Start writing down the formulas, what you know, and what you need to know.

 

[lightgrav]

If you slid ray 2 to the right a little, it would intersect with the central ray1 to form right triangles.
(I would also draw a "construction line" vertically from where ray 2 enters the top fluid)
The 2 "apparent depths" will show up along the 2 vertical lines.

 

[sylwesh98]

i don't know how to proceed from there! any clue please

 

[lightgrav]

The angle in the 2nd layer is less than the angle in the bottom layer ... about how many times as small? (this is a small-angle approximation)

How steep is the (blue) angle in air, in terms of the (red) angle in the bottom layer?
You're supposed to find the apparent depth (top left triangle + middle top triangle),
compared to the actual depth (big \| in gray + little \| in red).
each of these individual depth comparisons is just a ratio, whose formula you prob'ly know.

 

[sylwesh98]

i think only snells law is applicable in these cases.

 

[lightgrav]

In post 1 you said that you "knew it" if there was only 1 liquid ... did you not understand where that formula came from?
The small-angle approximation to Snell's law is :
n₁ θ₁ = n₂ θ₂ ... or ... n₁ tan θ₁ = n₂ tan θ₂

 

[sylwesh98]

but how it is applicable there?

 

[lightgrav]

do you forget what your goal is? either see (trial-and-error) which A value has apparent depth = ½ h , or
(generally) relate the apparent depth to the actual depth and the refractive index "A", and solve for A.
Snell relates the various θ , and tan θ ≈ the triangle width / height ... label the dimensions you know (or want).