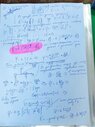SUMMARY
The discussion focuses on optimizing the polar axis for a dipole in polar coordinates, specifically addressing the electric potential and field equations. The potential is defined as $$V=\frac{1}{4\pi\epsilon_0}\frac{\mathbf{p}\cdot\mathbf{r}}{r^3}$$, while the electric field is given in coordinate-free notation as $$\vec{E}=\frac{1}{4 \pi \epsilon_0 r^5}(3 \vec{r} \vec{r} \cdot \vec{p}-r^2 \vec{p})$$. The key takeaway is the importance of selecting the correct polar axis to simplify the problem-solving process.
PREREQUISITES
- Understanding of electric dipole moments
- Familiarity with polar coordinates
- Knowledge of electric potential and field equations
- Basic grasp of vector calculus
NEXT STEPS
- Research the implications of electric dipole moments in electrostatics
- Study the derivation of electric potential from electric fields
- Learn about coordinate transformations in vector calculus
- Explore advanced topics in electrostatics, such as multipole expansions
USEFUL FOR
This discussion is beneficial for physics students, electrical engineers, and researchers focusing on electrostatics and field theory, particularly those working with dipole configurations in polar coordinates.