Orthogonality of Associated Laguerre Polynomial

[Muh. Fauzi M.]

I have a problem when trying to proof orthogonality of associated Laguerre polynomial. I substitute Rodrigue's form of associated Laguerre polynomial :

​

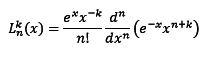
to mutual orthogonality equation :

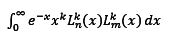
and set, first for

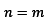and second for

.

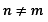But after some step, I get trouble with this stuff :

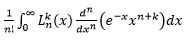
I've already search solution for this form but still no light. Any body here could help?

 

[ShayanJ]

The best way is using the differential equation. Write it for $L^k_n$ and $L^k_m$. Then multiply the first by $L^k_m$ and the second by $L^k_n$. Then subtract one from the other. Come back if you encounter a problem!

 

[Muh. Fauzi M.]

The best way is using the differential equation. Write it for $L^k_n$ and $L^k_m$. Then multiply the first by $L^k_m$ and the second by $L^k_n$. Then subtract one from the other. Come back if you encounter a problem!

Well I still didn't get it. $L^k_n$ has a rodrigues form and also associated Laguerre polynomial. Which one I need to use?

 

[ShayanJ]

Well I still didn't get it. $L^k_n$ has a rodrigues form and also associated Laguerre polynomial. Which one I need to use?

I said the differential equation, which is:
$x \frac{d^2 L_n^{k}}{dx^2} +(k+1-x) \frac{dL_n^{k}}{dx} +n L_n^k =0$

 

[Muh. Fauzi M.]

I said the differential equation, which is:
$x \frac{d^2 L_n^{k}}{dx^2} +(k+1-x) \frac{dL_n^{k}}{dx} +n L_n^k =0$

Nah... I got it. But still, I am stuck when connecting it with the orthogonality...

 

[ShayanJ]

Nah... I got it. But still, I am stuck when connecting it with the orthogonality...

I explained it in that post! Just write the equation two times for $L_m^k$ and $L_n^k$. Then multiply the first by $L_n^k$ and the second by $L_m^k$ and subtract one from the other. Then find an integrating factor and multiply the equation by it. You'll find out how to continue but come back if you didn't.