SUMMARY
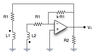
The discussion focuses on determining the oscillation amplitude in a linear oscillator circuit. Key calculations include the oscillation condition, KM ≥ L1 + L2, and the oscillation frequency, ω = R1/√(L1L2 - M²). It is established that the amplitude cannot be calculated directly from linear circuit analysis due to inherent non-linearities in the system, such as those from amplifiers or diode limiters. Approximations for amplitude can be explored through simulation tools like SPICE, considering factors like gain-bandwidth and saturation effects.
PREREQUISITES
- Understanding of linear circuit analysis
- Familiarity with oscillation conditions and frequency calculations
- Knowledge of non-linear circuit behavior, including amplifier saturation
- Experience with simulation software such as SPICE
NEXT STEPS
- Explore SPICE simulation techniques for oscillator circuits
- Research non-linearities in amplifiers and their impact on oscillation amplitude
- Study gain-bandwidth product and its implications in oscillator design
- Learn about Fourier series decomposition for signal analysis
USEFUL FOR
Electrical engineers, circuit designers, and students studying oscillator circuits and non-linear dynamics in electronics.