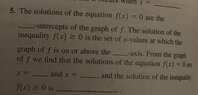Overcoming Struggles to Addressing Inequalities Step by Step

  • Context: MHB 
  • Thread starter Thread starter Seka88
  • Start date Start date
Click For Summary
SUMMARY

The discussion focuses on understanding inequalities in the context of the function notation \( f(x) \). Specifically, it clarifies that \( f(x) > 0 \) represents the portions of the graph above the x-axis, \( f(x) = 0 \) indicates points where the graph intersects the x-axis, and \( f(x) < 0 \) denotes areas below the x-axis. Participants seek a step-by-step approach to grasp these concepts, emphasizing the importance of defining \( f(x) \) for complete understanding.

PREREQUISITES
  • Understanding of function notation, specifically \( f(x) \)
  • Basic knowledge of graphing inequalities
  • Familiarity with the x-axis and y-axis in Cartesian coordinates
  • Concept of points of intersection in graphing
NEXT STEPS
  • Research the properties of inequalities in algebra
  • Study graphing techniques for functions and inequalities
  • Learn about the significance of critical points in functions
  • Explore step-by-step methods for solving inequalities
USEFUL FOR

Students learning algebra, educators teaching graphing concepts, and anyone seeking to improve their understanding of function inequalities.

Seka88
Messages
1
Reaction score
0
I’m overall struggling. Not liking the inequalities. Any step by step would be awesome
 

Attachments

  • D97F9FC9-ABA4-4A78-956C-B889286E4D18.jpeg
    D97F9FC9-ABA4-4A78-956C-B889286E4D18.jpeg
    241.5 KB · Views: 100
Last edited:
Mathematics news on Phys.org
$f(x) > 0$ is any part of the graph that is above the x-axis

$f(x) = 0$ is any part of the graph that crosses or touches the x-axis

$f(x) < 0$ is any part of the graph below the x-axis
 
Beer soaked query follows.
Seka88 said:
I’m overall struggling. Not liking the inequalities. Any step by step would be awesome
D97F9FC9-ABA4-4A78-956C-B889286E4D18.jpeg

Is there a specific inequality behind item #5?
 
Do you not understand that in "y= f(x)" any value of f is a "y" value? f(x)= 0 means y= 0 so that is a point on the x- axis. That is what goes into the first two blanks. For the other two we need to know how "f(x)" is defined here.
 
Last edited:

Similar threads

High School The same inequality, but two equivalent ways to express it
  • · Replies 14 ·
Replies
14
Views
2K
Undergrad A question about Young's inequality and complex numbers
  • · Replies 13 ·
Replies
13
Views
2K
MHB Finding an Alternative Solution to Doubtful Numerator Steps
  • · Replies 2 ·
Replies
2
Views
951
High School Missing out on intermediate algebraic steps
  • · Replies 23 ·
Replies
23
Views
2K
Undergrad Find an explicit formula for this n-sum problem
  • · Replies 7 ·
Replies
7
Views
3K
Prove this inequality using induction
  • · Replies 2 ·
Replies
2
Views
2K
MHB Number of steps of euclidean algorithm
  • · Replies 4 ·
Replies
4
Views
4K
Graduate Mathematics Behind Global Currency as a Wealth Inequality Regulation System
  • · Replies 26 ·
Replies
26
Views
2K
How many positive integers x satisfy this logarithmic inequality?
  • · Replies 3 ·
Replies
3
Views
3K
High School Looking for free graphing calculator for two-variable inequality
  • · Replies 4 ·
Replies
4
Views
2K