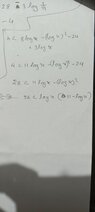- #1
Mr X
- 23
- 3
- Homework Statement
- How many positive integers x satisfy ##\log_{\frac x 8} (\frac{x^2} 4) < 7 + \log_2(\frac 8 x)##
- Relevant Equations
- Basic logarithamic rules
The whole solution is a bit long, which I'll attach but the part I'm stuck at is, assuming everything else above it is correct, is
4 < (log x - 3)(8-log x)
Note ; inequalities aren't technically taught yet in the course, so please try to make the solution not go too deep into that. If that isn't possible there's a high chance I've gone wrong before that step, hence I've uploaded the entire solution.
4 < (log x - 3)(8-log x)
Note ; inequalities aren't technically taught yet in the course, so please try to make the solution not go too deep into that. If that isn't possible there's a high chance I've gone wrong before that step, hence I've uploaded the entire solution.