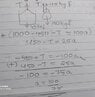Homework Help Overview
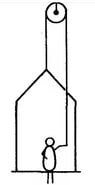
The discussion revolves around a physics problem involving a painter on a crate, focusing on acceleration and forces acting on a system, including a car and a lift. Participants are exploring the dynamics of the situation, particularly the application of free body diagrams (FBD) and the summation of forces.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation, Assumption checking
Approaches and Questions Raised
- Participants are attempting to solve parts of the problem using free body diagrams and force equations. There are questions about how to start the analysis, particularly for part a, and discussions about the correctness of the original poster's approach and assumptions.
Discussion Status
Some participants have provided guidance on drawing diagrams and writing force equations. There is acknowledgment of potential errors in the original poster's calculations and assumptions, particularly regarding the forces acting on the lift and the crate. Multiple interpretations of the problem are being explored, and some participants are reflecting on their understanding of the torque and forces involved.
Contextual Notes
There are indications of confusion regarding the signs and units in the force equations. The original poster's approach to acceleration and the forces involved is under scrutiny, with suggestions to clarify the setup and assumptions made in the problem.