Parallel RLC Circuit: Using General Impedance Equation

Click For Summary
SUMMARY

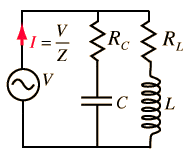
The discussion centers on the application of the general impedance equation for parallel RLC circuits, specifically when resistors are not directly in parallel with other components. The user inquires about substituting two resistors with an equivalent resistance and presents equations for the circuit's behavior. The circuit is an AC circuit, necessitating the use of reactance for capacitors (Xc = 1/ωC) and inductors (Xl = ωL) to derive the overall impedance from the two parallel arms: (Rc and C in series) and (Rl and L in series).

PREREQUISITES
  • Understanding of RLC circuit configurations
  • Knowledge of AC circuit analysis
  • Familiarity with reactance calculations for capacitors and inductors
  • Proficiency in using impedance equations
NEXT STEPS
  • Study the derivation of the general impedance equation for RLC circuits
  • Learn about series and parallel combinations of resistors, capacitors, and inductors
  • Explore the concept of equivalent resistance in complex circuits
  • Investigate the impact of frequency on reactance in AC circuits
USEFUL FOR

Electrical engineers, circuit designers, and students studying AC circuit theory who are looking to deepen their understanding of RLC circuit behavior and impedance calculations.

wetwilly92
Messages
8
Reaction score
0
Quick Question...

Given:
rlcpar.gif


Can I still use the general impedance equation for parallel RLC circuits even though the resistors are not in parallel with the other components? Substituting the two resistors for a single resistor with the equivalency resistance?
 
Physics news on Phys.org
The first leg is (Rc and C in series) and this combination is in parallel with (Rl and L in series)
 
technician said:
The first leg is (Rc and C in series) and this combination is in parallel with (Rl and L in series)

Does this give us...

1) Q2/C - ICRC - V = 0
2) ILRL - (L * diL/dt) - V = 0

Or am I just completely off?
 
The circuit is an AC circuit so you need to use Reactance of C... Xc =1/ωC to get an expression for the impedance of the Rc C arm.
You need to use Xl = ωL to get an expression for the Impedance of the Rl L arm
The overall impedance is these 2 impedances in parallel.
 

Thread 'Magnitude of buoyant force in fluids of different densities'

The book claims the answer is that all the magnitudes are the same because "the gravitational force on the penguin is the same". I'm having trouble understanding this. I thought the buoyant force was equal to the weight of the fluid displaced. Weight depends on mass which depends on density. Therefore, due to the differing densities the buoyant force will be different in each case? Is this incorrect?
View full post »

Similar threads

Impedeance of parallel RLC circuit
  • · Replies 3 ·
Replies
3
Views
2K
Resonant frequency of L - R||C circuit
  • · Replies 21 ·
Replies
21
Views
1K
Series RLC and Parallel RLC circuits
  • · Replies 15 ·
Replies
15
Views
5K
Combined tensions of an RLC series circuit with AC current
  • · Replies 3 ·
Replies
3
Views
1K
How Do You Calculate Capacitance in a DC Circuit with a Fully Charged Capacitor?
  • · Replies 3 ·
Replies
3
Views
2K
Phase difference RLC circuit
  • · Replies 5 ·
Replies
5
Views
3K
Finding parallel or in-series resistors
  • · Replies 3 ·
Replies
3
Views
823
Calculation of current in driven series RLC circuit
  • · Replies 8 ·
Replies
8
Views
2K
Quick question on Parallel RLC circuit (Conceptual)
  • · Replies 1 ·
Replies
1
Views
2K
How to determine if electrical components are connected in parallel or in series?
  • · Replies 10 ·
Replies
10
Views
1K