Parametrized Set .... McInerney, Example 3.3.3 .... ....

[Math Amateur]

I am reading Andrew McInerney's book: First Steps in Differential Geometry: Riemannian, Contact, Symplectic ... and I am focused on Chapter 3: Advanced Calculus ... and in particular on Section 3.3: Geometric Sets and Subspaces of $T_p ( \mathbb{R}^n )$ ... ...

In Section 3.3 McInerney defines what is meant by a parametrized set ... and then goes on to give some examples ...

... see the scanned text below for McInerney's definitions and notation ...

I need help with Example 3.3.3 which reads as follows:

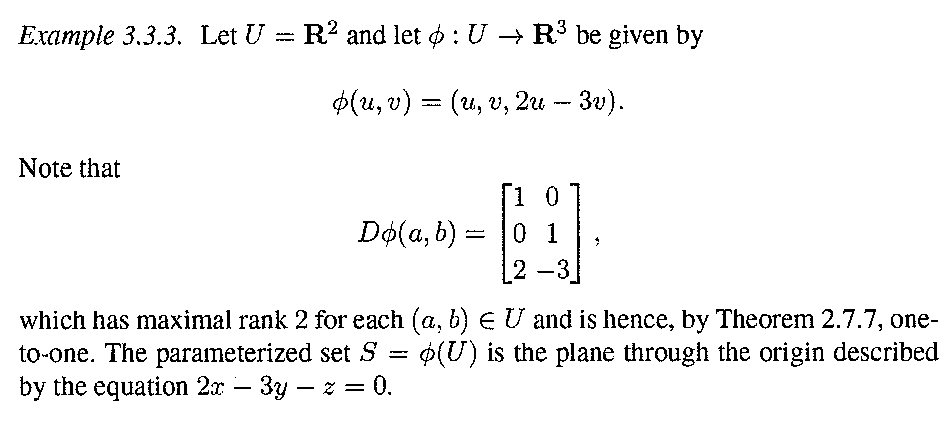
In the above example we read the following ... ..."... ... The parametrized set $S = \phi (U)$ is the plane through the origin described by the equation $2x - 3y - z = 0$ ... ... "Can someone please demonstrate how/why the parametrized set $S = \phi (U)$ is the plane through the origin described by the equation $2x - 3y - z = 0$ ... ... ?

Help will be much appreciated ... ...

Peter
*** EDIT ***

Reflecting on the above question we have $\phi (u, v) = ( u, v, 2u - 3v )$ ...

... so ... taking variable $(x, y , z)$ in $\mathbb{R}^3$ ... ...

... then for $u = x, v = y$ we have $z = 2x - 3y$ ...

But how exactly (rigorously) is $z = 2x - 3y$ the same as $\phi (U)$ ... ?

I am not happy with the above rough thinking/reasoning ...

Peter
=======================================================================================So that readers will understand McInerney's approach to parametrized sets and the relevant notation ... I am providing the relevant text at the start of Section 3.3 as follows ... ...

Hope that helps,

Peter

 

[fresh_42]

Can someone please demonstrate how/why the parametrized set $S = \phi (U)$ is the plane through the origin described by the equation $2x - 3y - z = 0$ ... ... ?

We have $\phi(U)=\{\,(u,v,2u-3v)\,|\,u,v \in \mathbb{R}\,\}=\{\,(x,y,z)\,|\,x,y\in \mathbb{R} \wedge 2x-3y-z=0\,\}$ which are the same sets. So the equation $2x-3y-z=0$ fully describes it: $x$ and $y$ are free parameters which together determine $z$, the same as in the $u,v$ notation.

 

[WWGD]

For the sake of completeness, $D\phi$ has rank 2 at every point. Just consider the first two lines, do that the plane is parametrized by $\mathbb R^2$. It may be helpful for you to consider cases that violate the conditions to see what a non parametrized set is like.