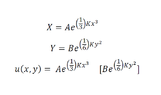emily600
- 2
- 0
Hi I'm having a bit of trouble with this question:
Use separation of variables to find all the possible separable solutions to the partial DE equation for u(x,y) given by
yux - 3x2 uy = 0 .I try u= X(x) Y(y)
ux = X'(x) Y(y)
uy = X(x) Y'(y)
which gives y(X' Y)-3x2(X Y')
then I divide by (XY) and rearrange it into y[X'/X] = 3x2 [Y'/Y]
which is equal to the separationconstant K (I think)
y[X'/X] = 3x2 [Y'/Y] = Kand from here I get a bit lost. I try a positive constant, so I get two equations.
yX'/X = + K rearranged into {X'= XK/y}
3x2Y/Y = + K rearranged into {Y'= YK/3x2 }
and then I try a negative constant with more or less the same equations resulting, but I'm not sure what to do with them?
Is this how you find all the possible solutions of the pde (trying both a positive and a negative constant)?
I'm told I can check the solution by substitution but I'm not sure how. Any help would be really appreciated.
Thanks
 .
.
Use separation of variables to find all the possible separable solutions to the partial DE equation for u(x,y) given by
yux - 3x2 uy = 0 .I try u= X(x) Y(y)
ux = X'(x) Y(y)
uy = X(x) Y'(y)
which gives y(X' Y)-3x2(X Y')
then I divide by (XY) and rearrange it into y[X'/X] = 3x2 [Y'/Y]
which is equal to the separationconstant K (I think)
y[X'/X] = 3x2 [Y'/Y] = Kand from here I get a bit lost. I try a positive constant, so I get two equations.
yX'/X = + K rearranged into {X'= XK/y}
3x2Y/Y = + K rearranged into {Y'= YK/3x2 }
and then I try a negative constant with more or less the same equations resulting, but I'm not sure what to do with them?
Is this how you find all the possible solutions of the pde (trying both a positive and a negative constant)?
I'm told I can check the solution by substitution but I'm not sure how. Any help would be really appreciated.
Thanks