A particle moving in a parabolic path in the ##x-y## plane

[brotherbobby]

Homework Statement

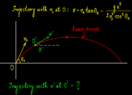
A particle moves in the $x-y$ plane with constant acceleration $a_0$ directed along the negative y–axis. The equation of motion of the particle has the form $y=px-qx^2$ where $p$ and $q$ are positive constants. Find the velocity of the particle at the origin of coordinates.

Relevant Equations

1. If $\dot x = v_x=\dfrac{dx}{dt}$ is the $x$ component of velocity and $\dot y = v_y=\dfrac{dy}{dt}$ the $y$ component of velocity, then the (scalar) velocity or speed at a point is given by $v = \left( \dot x^2+\dot y^2\right)^{\frac{1}{2}}$.
2. Acceleration components $a_x=\ddot x$ and $a_y=\ddot y$.
3. Acceleration can also be expressed as a function of position, for instance, $a_x=v_x\dfrac{dv_x}{dx}$.

Problem statement : I copy and paste the problem as it appears in the text down below. I have only changed the symbol of the given acceleration from $a\rightarrow a_0$, owing to its constancy.

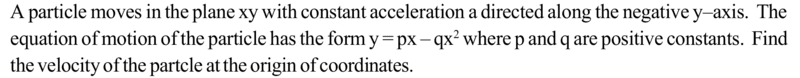
Attempt : I must admit that I could proceed very little.
Given $a_0=\dfrac{d^2y}{dt^2}\Rightarrow \dot y = a_0t+b$. But the constant $b$ is unknown.
Likewise, it is also given that $\dfrac{d^2x}{dt^2}=0\Rightarrow \dot x = c$, but the constant $c$ is unknown.

Differentiating the path of the particle $y = px-qx^2$ on both sides with respect to time, $\dot y = p\dot x-2qx\dot x\Rightarrow a_0t+b = pc-2qcx$.
This equation can yield the position $x$ as a function of the unknowns $b,c$.
Substituting for $x$ in the equation of the curve can yield $y$ again as a function of the same unknowns.

I can't see how to progress from here.

Request : A suggestion as to how to proceed to solve the problem will be welcome.

 

[PeroK]

Isn't that just projectile motion?

 

[brotherbobby]

Yes. But how to go about finding the velocity at the origin? The problem is set in a twisted way.

 

[PeroK]

You can write down $x$ and $y$ as functions of $t$ to get you started.

 

[Orodruin]

You already know that $x = v_x t$. This means that any derivatives with respect to $t$ may be rewritten as derivatives with respect to $x$ as $df/dt = v_x (df/dx)$. For the second derivative you would have $d^2f/dt^2 = v_x^2 (d^2f/dx^2)$. Use these relations for $f = y$ and evaluate at the origin. Poff, two unknowns ($v_x$ and $v_y$) and two equations.

 

[PeroK]

Hint. Take $t =0$ when the particle is at the origin.

 

[brotherbobby]

Hint. Take $t =0$ when the particle is at the origin.

How do we know that?

 

[brotherbobby]

You already know that $x = v_x t$. This means that any derivatives with respect to $t$ may be rewritten as derivatives with respect to $x$ as $df/dt = v_x (df/dx)$. For the second derivative you would have $d^2f/dt^2 = v_x^2 (d^2f/dx^2)$. Use these relations for $f = y$ and evaluate at the origin. Poff, two unknowns ($v_x$ and $v_y$) and two equations.

Yes, let me try.

 

[Orodruin]

How do we know that?

It is a freedom of choice. You can call whatever time you wish $t=0$.

 

[PeroK]

How do we know that?

We get to choose when to set our stopwatch to zero!

 

[Orodruin]

Hint. Take $t =0$ when the particle is at the origin.

However, I suggest not working with $t$ at all as mentioned above.

 

[erobz]

However, I suggest not working with $t$ at all as mentioned above.

The velocity of the particle at $t=0$ can be fully represented in terms of just $p$ and $q$? I'm having a mind block getting rid of $\dot x = c$ in the final result. (not trying to intrude, just looking for a "yes" or "no")

 

[PeroK]

The velocity of the particle at $t=0$ can be fully represented in terms of just $p$ and $q$? I'm having a mind block getting rid of $\dot x = c$ in the final result. (not trying to intrude, just looking for a "yes" or "no")

The answer should drop out from either method, although it's not a particularly enlightening problem, IMO.

 

[Orodruin]

The velocity of the particle at $t=0$ can be fully represented in terms of just $p$ and $q$? I'm having a mind block getting rid of $\dot x = c$ in the final result. (not trying to intrude, just looking for a "yes" or "no")

Yes, as long as acceleration is known.

 

[brotherbobby]

Hint. Take $t =0$ when the particle is at the origin.

Had a small question before I can attempt.

If indeed we are free to choose when the particle is at the origin (say at $t=0$), do we have a similar choice for a component of the velocity? I mean, can we instead choose $v_y(t=0)=0$?
Can we do so simultaneously $\rightarrow v_y=y=0\quad \text{at}\; t=0$?
We remember that $a_y\ne0$, so the above requirement will not force the particle to "sit" at the origin.

However, $a_x=0$ for the problem above. Hence we cannot choose $v_x(t=0)=x(t=0)=0$, for that will mean that the particle has no $x-$ displacement.
But that means we can make one of them zero, either $v_x$ or $x$ at time $t=0$.

Am I correct in my assertion above?

 

[PeroK]

Had a small question before I can attempt.

If indeed we are free to choose when the particle is at the origin (say at $t=0$), do we have a similar choice for a component of the velocity? I mean, can we instead choose $v_y(t=0)=0$?

Yes, but not both at the same time. Also, you have to know that $v_y = 0$ at some time. In general. it might never be zero.

Can we do so simultaneously $\rightarrow v_y=y=0\quad \text{at}\; t=0$?

Definitely not!

We remember that $a_y\ne0$, so the above requirement will not force the particle to "sit" at the origin.

However, $a_x=0$ for the problem above. Hence we cannot choose $v_x(t=0)=x(t=0)=0$, for that will mean that the particle has no $x-$ displacement.

$v_x = 0$ is a degenerate case, which you may wish to consider.

But that means we can make one of them zero, either $v_x$ or $x$ at time $t=0$.

$v_x$ depends in general on $p$ and $q$.

 

[brotherbobby]

Yes, but not both at the same time. Also, you have to know that vy=0 at some time. In general. it might never be zero.

Making $y=0$ at some time $t=0$ involves a translation of coordinates. Which is valid.
Why can't we do the same for $v_y$? Give our frame a boost equal to $v_y$ at time $t=0$ so that the particle has $v_y=0$ at time $t=0$.
Let me draw a projectile motion to help you see my point, mistaken though I might well be.

The path of the projectile is shown in red. At some point P, the projectile clearly as its position $y\ne 0$ and y-velocity $v_y\ne 0$. So I propose making a translation of the origin to some $O'$ such that $y'=0$. Likewise I propose giving this frame a boost equal to the particle's y-velocity $v_y$ such that the particle has velocity $v_y'=0$.(We'd discuss the situation with the $x-$components a bit later, let's focus on the $y-$ones for now)

 

[PeroK]

Making $y=0$ at some time $t=0$ involves a translation of coordinates. Which is valid.
Why can't we do the same for $v_y$? Give our frame a boost equal to $v_y$ at time $t=0$ so that the particle has $v_y=0$ at time $t=0$.

Yes, but the particle is no longer at the origin at $t = 0$. You can't transalte the coordinates without affecting the equation you were given: $y = px - qx^2$. That's a coordinate dependent equation.

 

[brotherbobby]

I think this is a very interesting point, and I am prepared to wait before solving the problem.

Yes, but the particle is no longer at the origin at $t = 0$. You can't transalte the coordinates without affecting the equation you were given: $y = px - qx^2$. That's a coordinate dependent equation.

We are given the equation of the curve along which the particle moves : $y = px-qx^2$. Nowhere is time mentioned. But the frame (of reference) is given - the particle clearly moves through the origin as $(0,0)$ is a solution to the curve.

Now comes the choice.

I choose $t=0$ when the particle is at $(0,0)$. I likewise choose $v_y=0$ at the time $t=0$. You might say that this gives the frame of reference a boost - but why am I not free to do that?

 

[Steve4Physics]

How about this...

Treat the system as a simple projectile launched from the origin $(0, 0)$ at $t=0$ ($a_0$ corresponds to $g$).

The apex of the trajectory (point P) is $(d, H)$ and the projectile reaches it at time T.

1) $y=px+qx^2$: find the value of $x$ which maximises $y$ (simple calculus). This is $d$. The corresponding maximum value of $y$ is $H$. Note that $d$ and $H$ are expressed in terms of $p$ and $q$..

2)The vertical component of velocity changes from its initial value $u_{0,y}$ to zero when $y$ changes from $0$ to $H$. That means $u_{0,y}$ can be found using a standard kinematics (‘suvat’) equation; then $T$ can be found. Note that $u_{0,y}$ and $T$ are expressed in terms of $p, q$ and $a_0$.
`
3) It’s now simple to find $u_{x,0}$ and hence $u$ (in terms of $p, q$ and $a_0$).

 

[PeroK]

I choose $t=0$ when the particle is at $(0,0)$. I likewise choose $v_y=0$ at the time $t=0$. You might say that this gives the frame of reference a boost - but why am I not free to do that?

Because now you've set $v_y = 0$ at the origin. You can check that this is invalid by looking for a counterexample. Any projectile motion with an initial velocity at the origin would do that. You can check that this satifies an equation of the form $y = px - qx^2$. $v_y$ would be zero at the apex: $(x_1, y_1)$. If we make this the origin, with $x' = x - x_1, \ y' = y - y_1$ we get the new equation:
$$y' + y_1 = p(x' + x_1) - q(x' + x_1)^2$$And this equation is not of the form $y' = px' - qx'^2$.

Whereas, a time translation $t' = t - t_0$ does not change the equation of the trajectory in the $x-y$ plane. So, you can take $t = 0$ at the origin without changing the equation you were given to work with.

 

[Orodruin]

Meanwhile I still would suggest not bothering to use the time parameter at all. It is a red herring.

 

[brotherbobby]

Thank you at @PeroK . I get your point.
But then it implies that the equation of the curve, viz. $y=px-qx^2$ is true only for a given (spatial) origin. We are really only free to choose time as we wish. A given $v_0$ at $(0,0)$ is non-negotiable.
Imagine I wanted to make the translation to some point $P (\ne O)$ along the trajectory $x\rightarrow x'=x+a,\quad y\rightarrow y'=y+b$. Here $(a,b)$ are the coordinates of $P$.
The new equation will not be of the form $y'=px'-qx'^2$, as you said. However, doesn't it seem counter-intuitive?
Surely, the particle has some velocity $v(P)$ at $P$. Could I not argue that the particle was actually launched from the point $P$ with the initial velocity $v(P)$? It will be the same curve, surely : $y=px-qx^2$. And yet, when we transform coordinates as I just did to the new origin $P$, it has a different equation!

 

[PeroK]

Thank you at @PeroK . I get your point.
But then it implies that the equation of the curve, viz. $y=px-qx^2$ is true only for a given (spatial) origin.

Precisely!

We are really only free to choose time as we wish. A given $v_0$ at $(0,0)$ is non-negotiable.
Imagine I wanted to make the translation to some point $P (\ne O)$ along the trajectory $x\rightarrow x'=x+a,\quad y\rightarrow y'=y+b$. Here $(a,b)$ are the coordinates of $P$.
The new equation will not be of the form $y'=px'-qx'^2$, as you said. However, doesn't it seem counter-intuitive?
Surely, the particle has some velocity $v(P)$ at $P$. Could I not argue that the particle was actually launched from the point $P$ with the initial velocity $v(P)$? It will be the same curve, surely : $y=px-qx^2$. And yet, when we transform coordinates as I just did to the new origin $P$, it has a different equation!

It can't be the same equation for a translation of your $x, y$ coordinates. You can see that in general for any graph in the $x-y$ plane.

 

[brotherbobby]

Precisely!

It can't be the same equation for a translation of your $x, y$ coordinates.

I get that, But "see" the curve for a minute. It is identical with $P$ as the origin as it is with $O$ as the origin.
If the curve is the same, why does it have a different equation in $x'$ and $y'$ when both the coordinate axes are parallel to the original $x-y$ axes?
Same curve has a different equation upon change of coordinate origin? So it seems to be.

 

[PeroK]

Same curve has a different equation upon change of coordinate origin? So it seems to be.

It must. Even the equation of a straight line changes if you translate the $x$ and/or $y$ coordinates.

 

[nasu]

Yes. But how to go about finding the velocity at the origin? The problem is set in a twisted way.

Do you know how the equation of trajectory looks like for projectile motion? What are the p and q constants in it?

 

[brotherbobby]

It must. Even the equation of a straight line changes if you translate the $x$ and/or $y$ coordinates.

I agree. In $y=mx+c$, $c$ is well-known to be the $y-$intercept. "Move" the coordiates a distance of $c$ vertically and the equation of the same line is $y'=mx'$. Rotate the axes and even $m'$ will change.

However, I think the present conundrum requires a mathematical working out, not least because of its non-intuitive nature. I draw below for you what I have in mind - but briefly, it is this :

"If I transform the equation of the trajectory for a projectile, viz. $y = x\tan\theta-\dfrac{gx^2}{2v_0^2\cos^2\theta}$ where the quantities have their usual meanings, from the present origin $O$ to a new origin $O'(a,b)$ along the trajectory, and suitably use the new angle to the horizontal $\theta' (<\theta_0)$ and new initial velocity $v'(<v_0)$, will it alter the form of the equation from $y'=x'\tan\theta'-\dfrac{gx'^2}{2v'^2\cos^2\theta'}$?"Of course my intuition tells me it shouldn't, wrong though I know it is. The drawing below shows my confusion:

We have for the new velocity $v'=(v'^2_x+v'^2_y)^{\frac{1}{2}}$ where $v'_x=v_{0x}=v_0\cos\theta_0$ and $v'_y=(v^2_{0y}-2gb)^{\frac{1}{2}}$ and $v_{0y}=v_0\sin\theta_0$.

Likewise for the new angle $\tan\theta'=\dfrac{v'_y}{v'_x}$.

Already I can see your point, in that there is a $b$ of the new coordinate origin appearing in the equation but nowhere the $a$ of the new origin. Is it possible that the $b's$ will cancel out with one another, or with the $a's$ where they are related by $b = a\tan\theta_0-\dfrac{ga^2}{2v^2_0\cos^2\theta_0}$? I have to calculate to find out.

 

[brotherbobby]

Do you know how the equation of trajectory looks like for projectile motion? What are the p and q constants in it?

Sure. $p=\tan\theta_0$ and $q = \dfrac{g}{2v_0^2\cos^2\theta_0}$

 

[nasu]

Then what else do you need to find velocity at time t=0? What is the $v_0$ in the expression for q?