Johnson Chou
- 4
- 0
<Moderator's note: Moved from a technical forum and thus no template.>
Hi everyone,
I have encountered a partial differential equation with square roots which I don't have a clue in solving it. After letting z=F(x)+G(y), I can't really figure out the next step. I tried squaring both sides but the square root still exists. Any help would be appreciated, thank you!
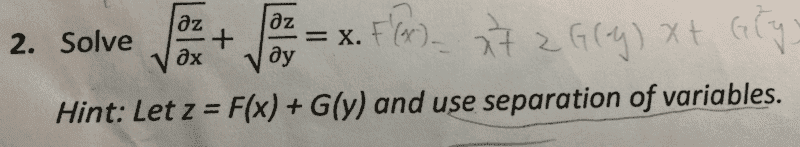
Hi everyone,
I have encountered a partial differential equation with square roots which I don't have a clue in solving it. After letting z=F(x)+G(y), I can't really figure out the next step. I tried squaring both sides but the square root still exists. Any help would be appreciated, thank you!
Attachments
Last edited by a moderator:
