Martyn Arthur
- 128
- 25
- Homework Statement
- Trying to get to fxx
- Relevant Equations
- Please see screen print
Hi;
please see below I am trying to understand how to get to the 2 final functions. They should be the same but 6 for the first one and 2 for the second?
(I hope my writing is more clear than previously)
There is an additional question below.
thanks
martyn
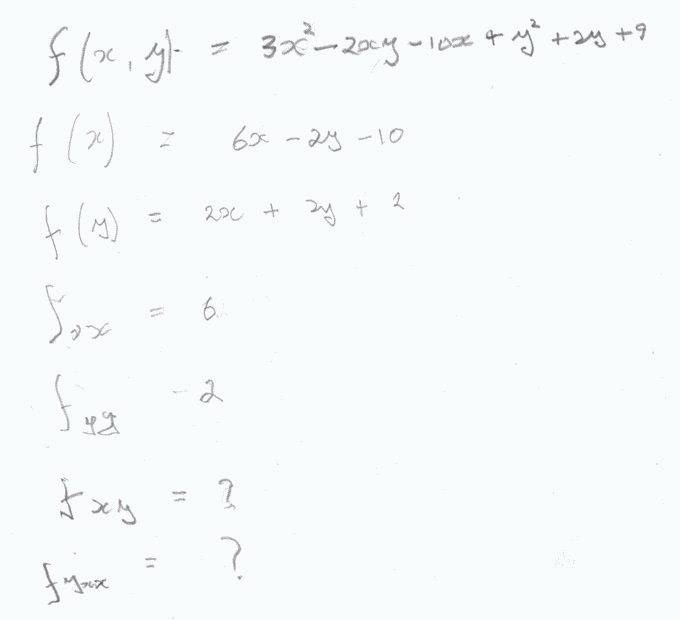
I can't find a standard derivative for cos^2 theta?
please see below I am trying to understand how to get to the 2 final functions. They should be the same but 6 for the first one and 2 for the second?
(I hope my writing is more clear than previously)
There is an additional question below.
thanks
martyn
I can't find a standard derivative for cos^2 theta?