Partial Surface Area of a Tube

[deweyirl]

Hi all,

I hope this is the correct place to post this.

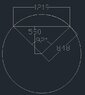
Below is a section of a pipe. The pipe has a radius of 0.848 m.

For this example, assume the pipe is buried below ground but a section of it remains exposed. The centre of the pipe is buried 0.590 mbelow the ground. If we assume the pipe is 1.00 m in length, what I am wanting to know is, how is the surface area of the exposed pipe calculated?

I know the surface area of the pipe would be 2 times pi times the radius times the length of the pipe.
The total surface area of the pipe would be 5.64 m2.

Thanks in advance

 

[jedishrfu]

You know the circumference right $2\pi r^2$ ?

and that a circle has 360 degrees but you're only interested in 92 degrees.

 

[sysprog]

$-$ removed $-$

 

[Lnewqban]

...
The centre of the pipe is buried 0.590 mbelow the ground. If we assume the pipe is 1.00 m in length, what I am wanting to know is, how is the surface area of the exposed pipe calculated?
...

For other cases for which you don't have a tool that can give you the angle, this may help:
https://en.wikipedia.org/wiki/Circular_segment

 

[osilmag]

Deweyirl. What is the "1219" number in your drawing? That might be the arc length of the exposed pipe or the side if were to be cut and stretched out to make a square.