Partition function of a particle with two harmonic oscillators

[mjmnr3]

Homework Statement

Consider now a particle, which can sit in two harmonic oscillators. Oscillator A has
energy levels ε=nhω, and oscillator B has energy levels ε= ε_0 + nhω, where ε_0 > 0 and
n = 0, 1, 2, . . .. The particle can hop freely between the two oscillators, and the available
states for the particle are therefore the harmonic oscillator levels in A and B.

Question b:
Give an expression for the partition function for the particle, when the temperature is T.
What is the probability P that the particle sits in oscillator A?

Relevant Equations

$$
z=\sum_{s} e^{-E(s) / k T}
$$

Here is the solution I have been given:

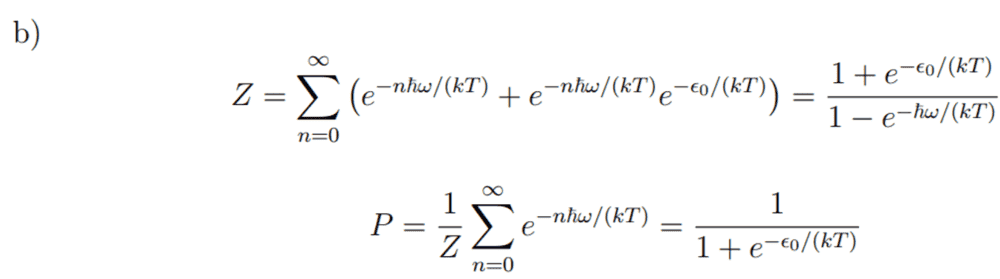
But I really don't understand this solution. Why can I just add these two exponential factors (adding two individual partition functions?).-------------------------------------------------------------------------------------------------------------------------------------

if $E_{A}=n \hbar \omega$ and $E_{B}=n \hbar \omega+\epsilon_{0},$ Why is
$$
z=\sum_{n=0}^{\infty} e^{-E_{A} / k T}+\sum_{n=0}^{\infty} e^{-E_{B} / K T}=Z_{A}+Z_{B}
$$
Because I would solve it differently. The way Daniel Schroeder (Introduction to thermal physics) teaches you to calculate the partition function is:
$z=\sum_{s}^{\infty} e^{-E(s) / k T}$, where $s$ is the different quantum states of the system. So how does the two exponential factors appear?

I interpret the system's hamiltonian consisting of a sum of the two harmonic oscillators $$\mathrm{H}=\mathrm{H}_{\mathrm{A}}+\mathrm{H}_{\mathrm{B}}$$, So what I should really find is the eigenvalues to this operator:
$$\hat{H}|s\rangle=E(s)|s\rangle$$
if $H_{A}$ and $H_{B}$ commutes, then they should have simultaneous eigenfunctions and we should expect the energy to be the sum of each hamiltons eigenvalue: $E(s)= E_{A}+E_{B}$
So in that case, the partition function would be:
$$
z=\sum_{n=0}^{\infty} e^{-\left(E_{A}+E_{B}\right) / \kappa T}=\sum_{n=0}^{\infty} e^{-E_{A} / k T} e^{-E_{B / K T}}=\sum_{n=0}^{\infty}\left(e^{-n \hbar \omega /(k T)} e^{-n \hbar \omega /(k T)} e^{-\epsilon_{0} /(k T)}\right)
$$
So the issue, is probably that I really don't understand the setup of this system, and what they mean by one particle and two harmonic oscillators.

 

[mjmnr3]

Here is the full problem text:

I use "An introduction to thermal physics" by Daniel V. Schroeder, If you prefer to refer directly to the litterature.

 

[TSny]

For the system in question b, the possible states of the particle are the states of oscillator A as well as the states of oscillator B. So, the possible energies of the particle in question b are the energy levels of A and the energy levels of B.

Note that the energy levels for part b are not the sum of the energies of oscillator A and oscillator B. The energy levels in part b are all the energy levels of A and all the energy levels of B.