SUMMARY
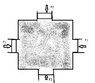
The discussion centers on Pascal's Law and its application to a symmetrical container with four pistons, each exerting force F on the fluid. The key conclusion is that the increase in pressure at the center of the container is F/A, not 4F/A, because pressure is defined as the perpendicular force per unit area applied to a fluid. This highlights that pressure is an intensive variable, independent of the size of the system, and is treated as a scalar quantity, which resolves the confusion regarding vector forces.
PREREQUISITES
- Understanding of Pascal's Law and its implications in fluid mechanics.
- Basic knowledge of pressure definitions and calculations.
- Familiarity with intensive and extensive properties in thermodynamics.
- Concept of scalar and vector quantities in physics.
NEXT STEPS
- Study the principles of fluid mechanics, focusing on Pascal's Law.
- Learn about intensive and extensive properties in thermodynamics.
- Explore the mathematical treatment of pressure as a scalar quantity.
- Investigate real-world applications of pressure in hydraulic systems.
USEFUL FOR
Students studying physics, particularly those focusing on fluid mechanics, as well as educators and professionals seeking to deepen their understanding of pressure dynamics in fluids.