fordy314
- 6
- 0
Pascal's principle hydraulic lift with torque involved(need help with lever)
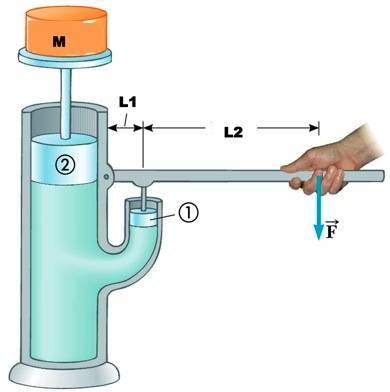
The mass is supported by piston 2 which has a mass of 0.250 kg and an area of 40.2 cm2 . A force is applied by the lever on piston 1 which has a mass of 0.085 kg and an area of 14.2 cm2.
The distance between the hinge and piston 1 is 4.47 cm. A force is applied a further 16.4 cm from piston 1.
What is the magnitude of the force F which must be applied to support the mass? You may neglect the mass of the fluid. You may also wish to TORQUE to someone about this problem.
ρ=m/v
P=F/A
P=Po+ρgh
Any relevant torque equations (not that far yet)
I'm pretty lost here, but I know that I need to find the force exerted by piston1.
The force required to lift the mass and piston2 is:
30.95kg*9.81m/s^2 = 303.6N
P=F/A=303.6N/(pi*.402^2)=598(k?)Pa
This is where I get lost. normally I would take P=Po+ρgh to find the pressure on piston 1 to find the force needed to push against it, but I don't have the height. Am I missing something, or do you think that I'm supposed to assume that they're at the same height?
Thanks.
Homework Statement
A hydraulic jack is used to support a mass which has a mass of 30.7 kg.The mass is supported by piston 2 which has a mass of 0.250 kg and an area of 40.2 cm2 . A force is applied by the lever on piston 1 which has a mass of 0.085 kg and an area of 14.2 cm2.
The distance between the hinge and piston 1 is 4.47 cm. A force is applied a further 16.4 cm from piston 1.
What is the magnitude of the force F which must be applied to support the mass? You may neglect the mass of the fluid. You may also wish to TORQUE to someone about this problem.
Homework Equations
ρ=m/v
P=F/A
P=Po+ρgh
Any relevant torque equations (not that far yet)
The Attempt at a Solution
I'm pretty lost here, but I know that I need to find the force exerted by piston1.
The force required to lift the mass and piston2 is:
30.95kg*9.81m/s^2 = 303.6N
P=F/A=303.6N/(pi*.402^2)=598(k?)Pa
This is where I get lost. normally I would take P=Po+ρgh to find the pressure on piston 1 to find the force needed to push against it, but I don't have the height. Am I missing something, or do you think that I'm supposed to assume that they're at the same height?
Thanks.
Last edited: