Paschen-Back and Zeeman in different base

[Dreak]

Hello,

In the image below, we see the result of the Zeeman and Paschen-Back effect in a magnetic field which we worked out, together with the exact result, described in different basesets (coupled J,m_j and uncoupled m_lm_s).

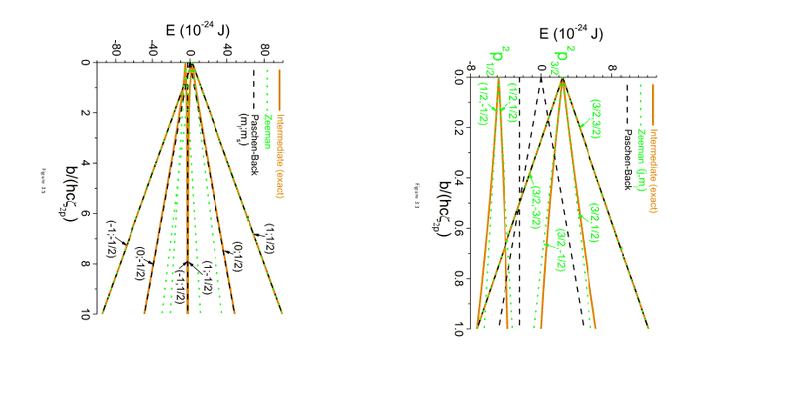
I understand that each effect can be better described in a different set, but I don't understand how that the result can be so 'wrong' compared to the exact result by using this different base.

I thought it was possible to go from coupled to uncoupled and visa versa, doesn't this also mean that an effect has to give the same results in a different base? Where does these errors come from?


I hope my question is clear enough :X

 

[DrDu]

How exactly did you "work it out"? Do you refer to a perturbational treatment?

 

[Dreak]

How exactly did you "work it out"? Do you refer to a perturbational treatment?

yes.

For example PB:

H(0) = H_Bohr + H_Zeeman
H(1) (perturbation Hamiltonian) = H_SO (spin orbit coupling)

with H_Zeeman = b(l_z = g_e.s_Z

and H_SO = l.s = 1/2(l_+s_- + l_-s_+) + l_z.s_z

 

[DrDu]

What you probably did was not using different bases but different zeroth order hamiltonians which have the corresponding basefunctions as eigenstates.
The perturbation series obtained starting from different zeroth order hamiltonians may differ dramatically. Using one H_0 already a first order correction may be sufficient to obtain a very good approximation to the exact eigenstates and energies while with another H_0 the perturbation series may be highly divergent.

 

[Dreak]

What you probably did was not using different bases but different zeroth order hamiltonians which have the corresponding basefunctions as eigenstates.
The perturbation series obtained starting from different zeroth order hamiltonians may differ dramatically. Using one H_0 already a first order correction may be sufficient to obtain a very good approximation to the exact eigenstates and energies while with another H_0 the perturbation series may be highly divergent.

Ah yes, seems a fitting explanation, thanks! :)