MaZnFLiP
- 16
- 0
[SOLVED] Pendulum and Centripetal Motion Question
Picture and FBD
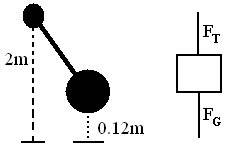
The Problem/Question
Calculate the speed of a 2.0m length pendulum at the very bottom of the swing if you raise it a vertical height of 0.12m
Relevant equations
F_net = F_T + F_G = F_C = m(\frac{V^2}{r})
The attempt at a solution
Well, after looking over this problem, I think I'm doing something amazingly wrong.
Looking at My equations, I went from
F_C = F_T + mg
to
m(\frac{V^2}{r}) = F_T + mg
From there I got:
\frac {V^2}{r} = F_T + g because the masses cancel.
Next:
V^2 = gr + F_T
After finding (-9.81\frac{m}{s}^2)(2.0m) = 19.62, I found the square root which was 4.429 \frac {m}{s}^2
The problem is that after looking at the answer sheet, The answer is supposed to be:
1.5\frac{m}{s}^2
Could someone please help as to tell me where I went wrong?
Picture and FBD
The Problem/Question
Calculate the speed of a 2.0m length pendulum at the very bottom of the swing if you raise it a vertical height of 0.12m
Relevant equations
F_net = F_T + F_G = F_C = m(\frac{V^2}{r})
The attempt at a solution
Well, after looking over this problem, I think I'm doing something amazingly wrong.
Looking at My equations, I went from
F_C = F_T + mg
to
m(\frac{V^2}{r}) = F_T + mg
From there I got:
\frac {V^2}{r} = F_T + g because the masses cancel.
Next:
V^2 = gr + F_T
After finding (-9.81\frac{m}{s}^2)(2.0m) = 19.62, I found the square root which was 4.429 \frac {m}{s}^2
The problem is that after looking at the answer sheet, The answer is supposed to be:
1.5\frac{m}{s}^2
Could someone please help as to tell me where I went wrong?