member 731016
- Homework Statement
- I try to derive coordinates for a mass on a rotating pendulum using a different coordinate system
- Relevant Equations
- $$(x,y)$$
For this problem,
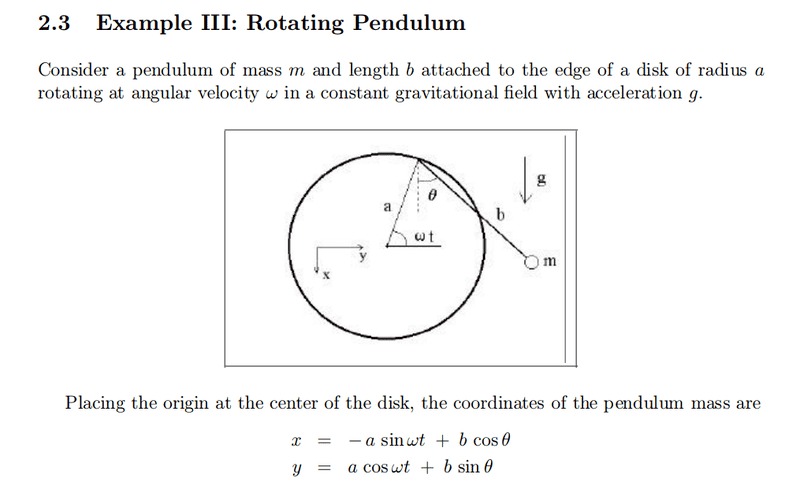
I correctly got the same coordinates for the pendulum mass using another coordinate system. The coordinate system I used was the other coordinate system rotated counterclockwise by 90 degrees. Why is the pendulum mass coordinates invariant in my cartesian coordinate system (x̄,ȳ)?
Thanks for any help!
I correctly got the same coordinates for the pendulum mass using another coordinate system. The coordinate system I used was the other coordinate system rotated counterclockwise by 90 degrees. Why is the pendulum mass coordinates invariant in my cartesian coordinate system (x̄,ȳ)?
Thanks for any help!