- #1
Gh778
- 421
- 0
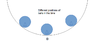
I would like to study a pendulum in 2D, not on Earth but only with one fixed mass attract a disk. Considered this fixed mass like a point. No friction on this theoretical study. The disk can move only around a part of circle. There are only 2 forces, F the attraction and N the force from wall (circle). The disk is composed with homogenous material, same density everywhere. The center of mass is fixed and it is in the center of circle of the disk. The center of gravity change always:
- it is more at center when the disk is far away the fixed mass
- it is more at outer circle of the disk when the disk is closed to the fixed mass
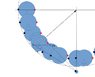
When I draw the trajectory of the center of gravity, it's not a circle. This would say the force from wall works.
But N seems to reduce the attraction F due to the non circle trajectory. So, I thought the energy goes to the angular velocity but N anf F don't give a torque because they pass trought the center of mass.
I tested an example with Algodoo software (2D software), and it confirm no rotation of the disk, it confirm too the lost of energy, sure it's not a professionnal software, maybe it's an error, like me the software see a non circle trajectory. I put an example, Algodoo is a free software.
images:
f1: the system
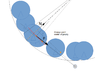
f2: 3 positions of disk (examples)
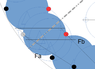
f3: N and F forces, orange point is the center of gravity
So,
1/ The disk have a torque or not ?
2/ The trajectory of the center of gravity is perpendicular to the force from wall or not ?
- it is more at center when the disk is far away the fixed mass
- it is more at outer circle of the disk when the disk is closed to the fixed mass
When I draw the trajectory of the center of gravity, it's not a circle. This would say the force from wall works.
But N seems to reduce the attraction F due to the non circle trajectory. So, I thought the energy goes to the angular velocity but N anf F don't give a torque because they pass trought the center of mass.
I tested an example with Algodoo software (2D software), and it confirm no rotation of the disk, it confirm too the lost of energy, sure it's not a professionnal software, maybe it's an error, like me the software see a non circle trajectory. I put an example, Algodoo is a free software.
images:
f1: the system
f2: 3 positions of disk (examples)
f3: N and F forces, orange point is the center of gravity
So,
1/ The disk have a torque or not ?
2/ The trajectory of the center of gravity is perpendicular to the force from wall or not ?
Attachments
Last edited: