MHB Percentage question reall EASY for you.

[mark321]

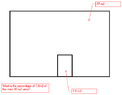
Can you help me figure out a percentage of an opening in a wall that is 87 m²?

What percentage is the smaller opening (door and a window: 7.8 m²) of the large wall?

Thanks,

I told you it was easy! :)

 

[Greg]

Hint: 3/4 = 0.75 and 3 is 75% of 4.

 

[mark321]

<Hint: 3/4 = 0.75 and 3 is 75% of 4. >

Sorry I don't get it.

The areas I have indicated are Square Meters - m2

 

[MarkFL]

<Hint: 3/4 = 0.75 and 3 is 75% of 4. >

Sorry I don't get it.

The areas I have indicated are Square Meters - m2

$x$ is the same percentage of $y$, no matter what kinds of quantities they represent, of course as long as they are both the same. It would of course be meaningless to ask what percentage of a kilogram a square meter is. For example 3 miles is 50% of 6 miles, just as 3 apples is 50% of 6 apples.

Look again at what greg1313 posted...how did he determine that 3 is 75% of 4? What arithmetic operation did he use?

 

[mark321]

View attachment 5456

View attachment 5457

Please refer to the attached Sketch. You guys sound like you know Math. Trust me when I say... I don't. Never did, since grade 6 it started to even get worse!

So of you guys would be so kind as to break this down.. youve heard of different books n diff topics for 'Dummies' then they have a set for 'Idiots'... Thats kind of where I'm at! :(

Thanks.

 

[Greg]

Percentage is a quantity out of 100. So, using the example I gave above, we have

$$\dfrac34=\dfrac{x}{100}$$

Solving for $x$ gives $x=75$, as follows:

$$\dfrac34=\dfrac{x}{100}$$

Multiply through by $100$:

$$\dfrac{300}{4}=x,\quad x=75$$

Using the quantities given in your problem we have

$$\dfrac{7.8}{87}=\dfrac{x}{100}$$

Can you solve for x? (A calculator will come in handy).

 

[mark321]

As much I'd really like to but I actually don't understand where x=75.
Where did the 75 come from. I have other areas I have to calculate Tomorrow morning so please feel free to demonstrate on the 87 m2 equation.

Thanks so much for breaking it down as u did!

It's all about the 75! But do I feel dumb!☺

 

[MarkFL]

As much I'd really like to but I actually don't understand where x=75.
Where did the 75 come from. I have other areas I have to calculate Tomorrow morning so please feel free to demonstrate on the 87 m2 equation.

Thanks so much for breaking it down as u did!

It's all about the 75! But do I feel dumb!☺

$$x=\frac{300}{4}=\frac{4\cdot75}{4}=\frac{\cancel{4}\cdot75}{\cancel{4}}=75$$

If I want to find what percentage $P$ that $a$ is of $b$, I would write:

$$P=\frac{a}{b}\cdot100$$

This tells me to take $a$, divide it by $b$, then multiply that quotient by 100.

If you solve the equation greg1313 gave you:

$$\dfrac{7.8}{87}=\dfrac{x}{100}$$

for $x$ (using the same steps he showed you when getting $x=75$), that's what the resulting formula would in effect instruct you to do. :)