Periodic solutions in a mechanical system

[wrobel]

Consider the following mechanical system

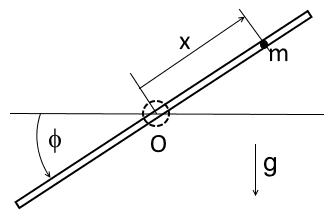
A thin tube can rotate freely in the vertical plane about a fixed horizontal axis passing through its centre $O$. A moment of inertia of the tube about this axis is equal to $J$. The mass of the tube is distributed symmetrically such that tube's centre of mass is placed at the point $O$.

Inside the tube there is a small ball which can slide without friction. The mass of the ball is $m$. The ball can pass by the point $O$ and fall out from the ends of the tube.

The system undergoes the standard gravity field $\boldsymbol g$

It seems to be evident that for typical motion the ball reaches an end of the tube and falls down out the tube. It is surprisingly, at least for the first glance, that this system has very many periodic solutions such that the tube turns around several times during the period.

For details see http://www.ma.utexas.edu/mp_arc/c/16/16-60.pdf
http://www.ma.utexas.edu/mp_arc/c/16/16-61.pdf

comments are welcome

 

[S.G. Janssens]

Very nice system, thank you. If I find the time, I could study the manuscript.

Would it be possible to produce some numerical simulations as well, so readers can visualise this counterintuitive motion? If you could do that, and you could give the gist of the proof without all technical details (which I like, but may be a bit too much), perhaps it is a good candidate for an "insight"? It is merely an idea.

 

[wrobel]

Would it be possible to produce some numerical simulations as well, so readers can visualise this counterintuitive motion?

I do not think so, anyway to catch those solutions numerically or somehow else it is a much more complicated problem than one I solved. Consider it as a pure existence theorem

 

[S.G. Janssens]

I do not think so, anyway to catch those solutions numerically or somehow else it is a much more complicated problem than one I solved. Consider it as a pure existence theorem

That is all right, though I am still curious. Perhaps it would be possible to set up a suitable boundary value problem, the nontrivial solution(s) of which correspond(s) to the periodic orbits of the original system? The BVP may not enjoy uniqueness, but maybe this way you could catch at least some solutions numerically.

 

[wrobel]

I have not an idea how to do that.

UPD: http://www.ma.utexas.edu/mp_arc/c/16/16-61.pdf

 

[Vincenzo Tibullo]

This is a representation of one of the solutions, found with the NDSolve function of Mathematica, and by trial and error on the initial conditions:
https://dl.dropboxusercontent.com/u/503888/file.gif

 

[wrobel]

Yes, such a type solution can be found by linearization of system (1.1) near the equilibrium $\phi=0,\quad x=0$. But the article is about completely different periodic solutions. It is about the solutions such that the tube rotates several times during the period.

ious. Perhaps it would be possible to set up a suitable boundary value problem, the nontrivial solution(s) of which correspond(s) to the periodic orbits of the original system? The BVP may not enjoy uniqueness, but maybe this way you could catch at least some solutions numerically.

I believe it is possible to approximate the periodic solution by finite trigonometric polynomials and find their coefficients from the minimization problem from the article. In this case one must solve minimization problem for a function on finite
dimensional space. (Galerkin method)

 

[S.G. Janssens]

This is a representation of one of the solutions, found with the NDSolve function of Mathematica, and by trial and error on the initial conditions:

See the comment in post #7. Still, I think it is nice that you tried this out, thank you. I have no idea how difficult it is to just guess initial conditions that lie on a periodic orbit of the type discussed in the article. Did you try that, too?

I believe it is possible to approximate the periodic solution by finite trigonometric polynomials and find their coefficients from the minimization problem from the article. In this case one must solve minimization problem for a function on finite
dimensional space. (Galerkin method)

I think that would be an interesting addition to (or continuation of) what is already an interesting article.

 

[Vincenzo Tibullo]

See the comment in post #7. Still, I think it is nice that you tried this out, thank you. I have no idea how difficult it is to just guess initial conditions that lie on a periodic orbit of the type discussed in the article. Did you try that, too?

I'm trying, but no luck, probably also due to the numerical errors of the algorithm internally used by the Mathematica function.

 

[Vincenzo Tibullo]

Another possible motion

https://dl.dropboxusercontent.com/u/503888/file2.gif

and the corresponding time diagrams

https://dl.dropboxusercontent.com/u/503888/graphics.png

 

[wrobel]

o great thanks!

 

[Orodruin]

I am guessing that these orbits are unstable? Or are there any stable orbits as well?

 

[tionis]

A thin tube can rotate freely in the vertical plane about a fixed horizontal axis passing through its centre $O$.

There is a rod going through the center of the tube? How can the ball pass from one side to the other?

 

[Orodruin]

There is a rod going through the center of the tube?

What makes you think that? "Axis" is not the same as "rod". There is absolutely nothing in the problem that suggests this and it is anyway a trivial construction to make without the rod through the centre. The less trivial part is "frictionless". This is an A-level thread, please treat it as such.

 

[tionis]

What makes you think that? "Axis" is not the same as "rod". There is absolutely nothing in the problem that suggests this and it is anyway a trivial construction to make without the rod through the centre. The less trivial part is "frictionless". This is an A-level thread, please treat it as such.

Ah, ok. Thanks for clearing that up.

 

[Vincenzo Tibullo]

I am guessing that these orbits are unstable? Or are there any stable orbits as well?

What do you mean by "stable"? Given that $\theta$ increases (or decreases) at each time interval of length $\omega$, this is not a motion around an equilibrium position, so the usual concept of stability of an equilibrium position does not apply.

 

[Orodruin]

What do you mean by "stable"?

That for any point in phase space on the periodic orbit, there exists a neighbourhood such that any point in that neighbourhood is part of a periodic orbit.

I am talking about orbital stability, not stability in terms of a stationary point of the system.

 

[S.G. Janssens]

What do you mean by "stable"? Given that $\theta$ increases (or decreases) at each time interval of length $\omega$, this is not a motion around an equilibrium position, so the usual concept of stability of an equilibrium position does not apply.

That for any point in phase space on the periodic orbit, there exists a neighbourhood such that any point in that neighbourhood is part of a periodic orbit.

I am talking about orbital stability, not stability in terms of a stationary point of the system.

If you prefer to talk about stability of points instead, you could reduce the problem of (in)stability of the periodic orbit to (in)stability of the fixed point of a suitably defined Poincaré map.

 

[mfb]

@Vincenzo Tibullo: Great example.

Can you share the inital values?
For the easiest motion (k=0) I found x=1, θ=0.4622, $\dot x = \dot \theta = 0$ at t=0. It is unstable, not surprising I think. I would expect all solutions to be unstable.

I wonder how solutions with very large k and small ω look like. Wild rotations with tiny motion of the masses, but how does that give a periodic orbit?