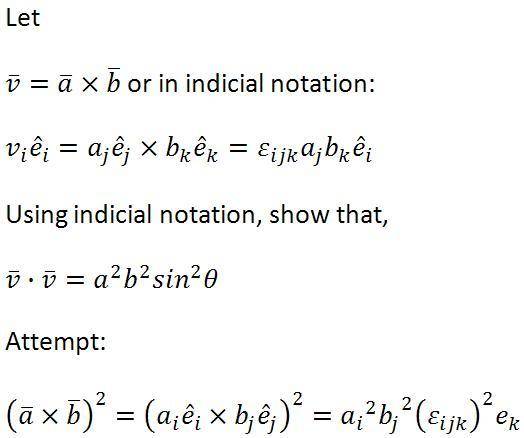SUMMARY
The discussion focuses on the complexities of using indicial notation in vector mathematics, particularly in the context of the permutation symbol and the Einstein summation convention. Participants clarify the importance of correctly handling dummy indices when squaring expressions involving the Levi-Civita symbol, \(\epsilon_{ijk}\). The angle \(\theta\) is identified as the angle between vectors \(\vec{a}\) and \(\vec{b}\), leading to the conclusion that the cross product magnitude is given by \(v = |\vec{a} \times \vec{b}| = ab \sin(\theta)\). The correct formulation of \(v_i^2\) is established as \(v_i^2 = a^2b^2\sin^2(\theta)\).
PREREQUISITES
- Understanding of indicial notation and tensor calculus
- Familiarity with the Levi-Civita symbol (\(\epsilon_{ijk}\))
- Knowledge of the Einstein summation convention
- Basic concepts of vector algebra, including cross products
NEXT STEPS
- Study the properties of the Levi-Civita symbol in depth
- Learn about the Einstein summation convention and its applications
- Explore vector calculus, focusing on cross products and their geometric interpretations
- Investigate advanced topics in tensor analysis and their relevance in physics
USEFUL FOR
Students and professionals in mathematics, physics, and engineering who are working with vector calculus and tensor analysis, particularly those dealing with indicial notation and the properties of the Levi-Civita symbol.