- #1
- 22,183
- 3,321
Part 1:
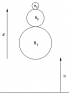
Consider ##n## balls ##B_1##, ##B_2##, ..., ##B_n## having masses ##m_1##, ..., ##m_n##, such that ##m_1\ll m_2\ll ...\ll m_n##. The ##n## balls are stacked above each other. The bottom of ##B_1## is a height ##h## above the ground, and the bottom ##B_n## is a height ##\ell## above the ground. The balls are dropped. In terms of ##n##, to what height does the top ball bounce. Assume the balls bounce elastically, assume there is no wind resistance, etc.
Part 2: Assume that ##h## is ##1## meter and assume ##\ell## is negligible. How big should ##n## be in order that the top one reaches a height of ##1## kilometer. How big should ##n##be in order that the top one reaches escape velocity? (Escape velocity is approximately ##11200~m/s##)
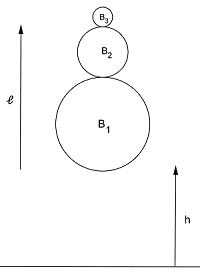
Consider ##n## balls ##B_1##, ##B_2##, ..., ##B_n## having masses ##m_1##, ..., ##m_n##, such that ##m_1\ll m_2\ll ...\ll m_n##. The ##n## balls are stacked above each other. The bottom of ##B_1## is a height ##h## above the ground, and the bottom ##B_n## is a height ##\ell## above the ground. The balls are dropped. In terms of ##n##, to what height does the top ball bounce. Assume the balls bounce elastically, assume there is no wind resistance, etc.
Part 2: Assume that ##h## is ##1## meter and assume ##\ell## is negligible. How big should ##n## be in order that the top one reaches a height of ##1## kilometer. How big should ##n##be in order that the top one reaches escape velocity? (Escape velocity is approximately ##11200~m/s##)