Pivoted beam with force at one end and spring attached to the other end

[snoopios]

Homework Statement

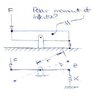
I've been set the task to come up with a solution/equation for a beam with a known mass (M) which is acted upon by a force (F) which is pivoted about a point. The other side of the beam is connected to the floor by a spring with a spring constant (k). What I'm trying to do is work out the angular acceleration of the beam.

Homework Equations

$\alpha=g \frac{m_1L_1-m_2L_2}{m_1L_1^2+m_2L_2^2}$

I have the equation above and know that m1 would techincally be my force (F). What I'm confused about is how to work out the angular acceleration of the beam which has a spring on the opposite side of the beam acting against the force (F) because surely, the spring basically mirrors the force (F) but in the opposite direction when it reaches a certain amount of extension and because of this, the masses are technically equal and therefore leads to the equation

$\alpha=g \frac{L_1-L_2}{L_1^2+L_2^2}$

Since the opposing force technically changes with respect to angular displacement and spring extension, surely this means that m2 is constantly changing?

What my end goal is, is to be able to come up with or get a formula that I can use in Microsoft Excel to create a data sheet where I can manipulate each value such as (spring constant, mass of beam etc.) and also find out the angular acceleration from different applied forces as well as theta values which I can then plot a graph of theta against time. I'm confusing myself with the first equation trying to apply it to a spring to be able to work out the angular acceleration.

Thanks in advance

 

[snoopios]

I've just realized (or actually thought about) that surely the spring force acting against the force acting on the beam is going to turn into some form of differential (i.e. spring force with respect to extension, or something like that, I'm not massively good at explaining things). So maybe something like ((Force * Distance to pivot)+(Mass of beam * Gravity * Centre of mass of beam to pivot length)) = ((Spring force / Extension (as some form of differential)). This is an entire guess but I think it makes sense. My attempt at some kind of solution is below;

$(F*L1)+(Mass of beam * 9.81 * 0.5 * L1) = \frac{\delta Spring Force}{\delta Spring length} * L2$

Like I said, this is a complete guess but I think I'm kind of on the right track seeing as if the input force is increased, the resistive force of the spring will increase and the length of the spring will increase proportionally to the forces.

 

[snoopios]

Um, I've just attached my spreadsheet. Does anyone know how I can use the Torque = Polar Moment of Inertia * Angular Acceleration equation to somehow incorporate the effect of the opposing spring force?