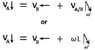Planar kinematics of rigid bodies

[tamtam402]

Homework Statement

Homework Equations

I'm dumbfounded by this problem. I can solve the (I think) harder problems with two fixed points and three rod segments. All the examples given in this book are of such "harder" problems and I have absolutely no example that resembles this problem to use as a reference. It is stated that I should solve the relative-velocity equations. This equation being:

Va = Vb + Va/b

(Velocity of A is equal to the Velocity of b + the apparent velocity of A as seen from B).

Please note that these are vectors.

I'm also aware of V = wr, which translates to V = w X r in vector form.

The Attempt at a Solution

I have no idea that to do. In all the other problems I had a fixed reference point that I could use. Here in the relative-velocity equation it seems like I only have one segment, how am I supposed to use the relative-velocity equation??!

I'm starting to think this is unsolvable using the requested equation.

Please help... thanks.

 

[Simon Bridge]

If you feel you need a fixed reference point to make sense of the situation, then just pick one.
How about the origin of the coordinate system?

 

[TSny]

Since you are asked to use concepts of relative velocity, start with your equation

$\vec{V}_A = \vec{V}_B + \vec{V}_{A/B}$

Can you state the exact direction of each of the three vectors in this equation?

 

[haruspex]

It's a bit unclear what it means by the relative velocity equations. I suggest taking velocities relative to G. You can certainly write down some interesting vector equations then. Do you see what G's path is? Can you write an equation which expresses that using the vector OG? Can you relate the vector OG to the vector GA using a unit vector in the y direction?

 

[tamtam402]

Guys I tried all your suggestions but I still cannot solve this... My exam is coming up soon and I am starting to get stressed out. The direction of Va is obviously -2j, Vb is -xi (unknown value) and Va/b is to the bottom and right, so something i + something j.

 

[tamtam402]

Also by writing this I realized I have the equation -2 = 0.173wba for the y direction since obviously point B has no vertical speed. I checked at the end of my book and that was the right answer. However, I would like to know why I cannot solve this problem by replacing the linear speed vectors with the cross products of the w X r form. By defining a fixed reference point on the bottom corner of the L shaped tunnel, I get this contradiction for Vb:

Vb = wob X rb

wob = (0,0,wob) and rb = (-0.2*cos(30),0,0)

This cross product gives Vb = (0,-0.173wob,0)... so now Vb has no horizontal speed and all its speed is vertical? What the heck is going on with this contradiction.

 

[TSny]

By defining a fixed reference point on the bottom corner of the L shaped tunnel, I get this contradiction...

The bottom corner of the L shaped tunnel is not the point of "instantaneous center of rotation" of the rod. Do you know how to find the center of rotation by using the known directions of V_A and V_B?

 

[haruspex]

Fwiw, my thinking was v_A = v_G + ω × r, where r is the vector from G to A. Similarly v_B = v_G - ω × r.
If O is the right angled corner, the vector OG can be written as 2r.j j - r, and this has constant magnitude. The derivative of that is v_G .
Don't know if any of that helps.

 

[TSny]

There are two common approaches to this type of problem:
(1) use relative velocity formulas such as $\vec{V}_A = \vec{V}_B + \vec{V}_{A/B}$
(2) find the instantaneous center of rotation 0 and use formulas such as $\vec{V}_A = \vec{\omega} \times \vec{r}_{A/0}$ where $\vec{r}_{A/0}$ is the position of point A relative to the instantaneous center of rotation.

The statement of the problem appears to ask you to solve the problem using only the first method, but you are to solve the relative velocity equations 2 ways:
(a) use the relative velocity formula to construct a velocity diagram and solve graphically.
(b) solve the relative velocity formula analytically (using components, say).

When setting up a relative velocity formula such as $\vec{V}_A = \vec{V}_B + \vec{V}_{A/B}$ , it is a good idea to explicitly show the directions as shown in the attached figure.

Try using this equation to construct a velocity diagram (vector addition diagram) showing how the three vectors are related in a right triangle. You can then find $\omega$ and and $V_B$ from the diagram.

The analytical method is to take components of the relative velocity equation. You already indicated that you did this for the vertical component to find $\omega$. See if you can find $V_B$ by considering the horizontal component.

To find $V_G$ now that you have $\omega$, set up a relative velocity formula for $V_G$, such as $\vec{V}_G = \vec{V}_A+ \vec{V}_{G/A}$. Again, you can solve this using a velocity diagram (but you won’t get a right triangle this time) or you can solve the equation analytically using components.