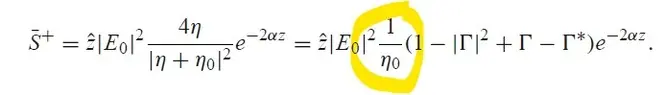baby_1
- 159
- 16
- Homework Statement
- Obtaning the Poynting vector for the conductor
- Relevant Equations
- Maxwell Equation
Hi,
Below are the expressions for the electric (E) and magnetic (H) fields in a good conductor.

Using those, the Poynting vector can be determined as follows.

By applying the appropriate conversions and starting from these equations, we obtain:


However, the result differs from the one in the book, where the relationship between the two intrinsic impedances is defined differently.

Below are the expressions for the electric (E) and magnetic (H) fields in a good conductor.
Using those, the Poynting vector can be determined as follows.
By applying the appropriate conversions and starting from these equations, we obtain:
However, the result differs from the one in the book, where the relationship between the two intrinsic impedances is defined differently.