Electromagnetic waves incident on an anti-reflective coating

[ContagiousKnowledge]

Homework Statement

A glass lens is coated with an anti-reflective coating. In air, he wavelength of light incident on the glass is λₒ. The index of refraction of the glass is n, and the index of refraction of the coating is √n. The refractive index of air is 1. Show that the coefficient of reflection for light normally incident on the lens is R=[((n-1)^2)cos^2[(π/2)(λₒ/λ)]/[4n+((n-1)^2)cos^2[(π/2)(λₒ/λ)]]

Comment on how successful the coating is at suppressing unwanted reflection of light incident on the lens.

Relevant Equations

An electromagnetic wave has electric component Eₓ(z, t) and magnetic component ZHᵧ(z, t) with amplitude Eₒ can be described by:

Eₓ(z, t) = Eₒcos(ωt - kz) = Eₜcos(ωt - kz) + Eᵣcos(ωt + kz)
ZHᵧ(z, t) = Eₒcos(ωt - kz) = Eₜcos(ωt - kz) - Eᵣcos(ωt + kz)

where Z is the impedance free space and Eₜ and Eᵣ are the amplitudes of the transmitted and reflected wave respectively.

We're trying to prove this:

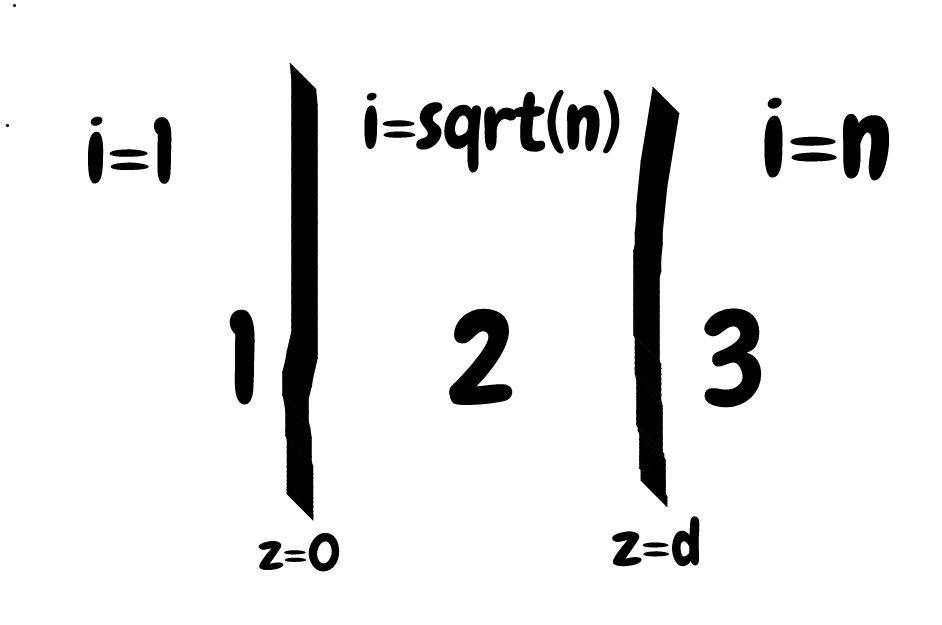
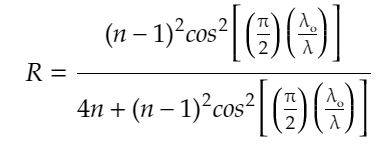There exists 3 distinct regions: Region 1 has index of refraction 1 and lies before light hits the coating. For simplicity, define the position of the interface between the air and the coating z=0. The second region is the coating, which has index of refraction √n. At position z=d lies the interface between the coating and the glass. Beyond this point lies region 3 with index of refraction n.

Let's say the amplitude Eₒ of the incident wave is one.

Eₓ1(z, t) = cos(ωt - kz) + Acos(ωt + kz) + Bsin(ωt + kz)

The corresponding magnetic component is:

ZHᵧ(z, t) = cos(ωt - kz) - Acos(ωt + kz) - Bcos(ωt + kz)

Where A and B are unknown constants and Acos(ωt - kz) + Bsin(ωt + kz) represents the the reflected wave. Since there is reflection of the boundary at z=0 and the boundary at z=d, and the reflected waves may not be in phase, the reflected waves may have sine and cosine components. We know that the math should turn out such that the reflected wave is only cosine-dependent, but we must account for the possibility of a sine component for the time being. We can't work backwards from the given conclusion.

Doing this analysis in all three regions yields the following.

Region 1:
Eₓ1(z, t) = cos(ωt - kz) + Acos(ωt + kz) + Bsin(ωt + kz)
ZHᵧ1(z, t) = cos(ωt - kz) - Acos(ωt + kz) - Bcos(ωt + kz)

Region 2:
Eₓ2(z, t) = Ccos(ωt - √(n)kz) + Dsin(ωt - √(n)kz) + Ecos(ωt + √(n)kz) + Fsin(ωt + √(n)kz)
ZHᵧ2(z, t) = √(n)[Ccos(ωt - √(n)kz) + Dsin(ωt - √(n)kz) - Ecos(ωt + √(n)kz) - Fsin(ωt + √(n)kz)]

Region 3:
Eₓ3(z, t) = Gcos(ωt - nk(z-d)) + Hsin(ωt - nk(z-d))
ZHᵧ3(z, t) = n[Gcos(ωt - nk(z-d)) + Hsin(ωt - nk(z-d))]

We currently have lots of equations and eight unknowns. We can try solving for some of the constants in terms of other constants. The electric and magnetic fields are continuous across the boundaries because the surface is presumably uncharged. I used Eₓ1(z, t)=Eₓ2(z, t) to determine 1 + A = C + E and B = D + F. A + B should yield the coefficient of reflection we're looking for. However, this method is incredibly tedious. I am not confident that this method would yield success, and I have limited time. Is there a more intelligent way to do this?

Update: I have solved for all of the constants in terms of the other constants. Now, I have eight unknowns and eight equations. However, the system of equations is very complicated. I don't think trying to solve it by hand is a viable option.

A = C+E-1
B=D+F
1-A=√(n)[C-E]
B=-√(n)[D-F]
G=Ccos(√(n)kd) + Dsin(√(n)kd)+Ecos(√(n)kd)+Fsin(√(n)kd)
H=Csin(√(n)kd)+Dcos(√(n)kd)-Esin(√(n)kd)+Fsin(√(n)kd)
√(n)G=Ccos(√(n)kd)-Dsin(√(n)kd)-Ecos(√(n)kd)-Fsin(√(n)kd)
√(n)H=Csin(√(n)kd)+Dcos(√(n)kd)+Esin(√(n)kd)-Fcos(√(n)kd)

There exists a formula R=[(n1-n2)/(n1+n2)]^2. If my reasoning is correct, the R we are trying to solve for is the sum of the reflection coefficients from both boundaries, so one could try plugging in 1 for n1 and √n for n2 for the first boundary and √n for n1 and n for n2 for the second boundary and summing the results. I'm just not sure how to solve for n in terms of useful constants.

 

[Charles Link]

The simplest way to do this is to use the Fresnel coefficients. The equations for the electric field amplitudes can then be solved as an infinite series of multiple reflections, or as a system of linear equations with a right going wave and a left going wave on each side of each interface, except for the final right going wave on the right side of the second interface. $\\$ It's extra work to derive the Fresnel coefficients. Read how they are derived, and use the result. Finally, once you get the ratio $E_{left \, going}/E_{right \, going}$ at the first surface, the energy reflection coefficient for the complete system is $R=|E_{left \, going}|^2/|E_{right \, going}|^2$. $\\$ One thing that I think you omitted is the thickness of the anti-reflection coating,(the thickness is a certain fraction of wavelengths), and that is also relevant in solving this. You need it to compute the phase of the components that travel across the coating and back, etc. Hint: What is the thickness $d$ in terms of $\lambda_o$ and $n_{coating}$?

 

[Charles Link]

A follow-on: I worked through the calculation in its entirety, and I was able to generate the same result that they have. This calculation is rather cumbersome algebraically, making it actually rather difficult, but you might find it worthwhile to work through it. I'd be happy to help you through some of the steps. To get started, you need to work through the tips given in post 2. $\\$ Additional comment: Conceptually, this problem is not very difficult. Learning how to treat the Fabry-Perot effect for thin films takes some effort, but once you do, you have the concepts that you need. Getting the result that they have is, however, a somewhat lengthy algebraic exercise. $\\$ Edit: Now that I worked through it, I think I can simplify the algebra for you.

 

[Charles Link]

The OP has yet to respond. @ContagiousKnowledge This is really a very good problem, and hopefully you follow it up. It took me about an hour to solve it, but I think I could lead you through it in a very systematic manner. It would be very good to learn how to work the Fabry-Perot etalon scenario, and this problem is a good exercise using it, with a practical application. $\\$ Edit: This one is most readily done with multiple reflections, which results in an infinite geometric series. The expression for $R$ has the form $R=r^2|1+\frac{ae^{i \theta}}{1+be^{i \theta}}|^2$. The rest is just algebra with complex numbers. One thing that results in the expression to get the answer that they give is that $a+b=1$. In addition, the trigonometric identity $\cos^2{\theta}=\frac{\cos(2 \theta)+1}{2}$ is needed to get the expression to the final form. $\\$ @Delta2 You might find this "Edit" of interest.