Please help solve the equation in black hole f(R) theories

[Boy_saber]

In the paper https://arxiv.org/abs/1210.4699. How to solve this equation?

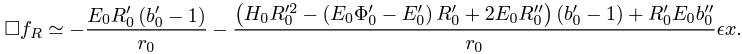
I've tried it, it's not same as in this paper. Even zero order still not the same.
This is what I try to do at zero order.

input

$$E=E_0\left(r_0\right)$$
$$H=H_0\left(r_0\right)$$
$$b=b\left(r_0\right)$$
$$R=R_0\left(r_0\right)$$
$$\Phi =\Phi _0\left(r_0\right)$$
$$r=r_0$$
$$g^{11}=1-\frac{b}{r}$$
$$\Box f_R=H g^{11} \left(\frac{\partial R}{\partial r_0}\right){}^2+E \left(\left(1-\frac{b}{r}\right) \left(\frac{\partial R}{\partial r_0} \left(-\frac{\partial \Phi }{\partial r_0}\right)+\frac{\frac{\partial R}{\partial r_0}}{r}+\frac{\partial }{\partial r_0}\frac{\partial R}{\partial r_0}\right)+\frac{\left(1-\frac{\partial b}{\partial r_0}\right) \frac{\partial R}{\partial r_0}}{r}\right)$$

output

$$-\frac{b\left(r_0\right) H_0\left(r_0\right) R_0'\left(r_0\right){}^2}{r_0}+\frac{b\left(r_0\right) E_0\left(r_0\right) R_0'\left(r_0\right) \Phi _0'\left(r_0\right)}{r_0}-\frac{E_0\left(r_0\right) b_0'\left(r_0\right) R_0'\left(r_0\right)}{r_0}-\frac{b\left(r_0\right) E_0\left(r_0\right) R_0'\left(r_0\right)}{r_0^2}-\frac{b\left(r_0\right) E_0\left(r_0\right) R_0''\left(r_0\right)}{r_0}+H_0\left(r_0\right) R_0'\left(r_0\right){}^2-E_0\left(r_0\right) R_0'\left(r_0\right) \Phi _0'\left(r_0\right)+\frac{2 E_0\left(r_0\right) R_0'\left(r_0\right)}{r_0}+E_0\left(r_0\right) R_0''\left(r_0\right)$$

Where did I make a mistake?

 

[member38644]

It is difficult to pinpoint the exact mistake without more context and information about the specific equation and problem being solved. However, it is possible that there may be a missing term or a sign error in the output equation. It is also important to carefully check all the inputs and their derivatives to ensure they are correct. It may also be helpful to consult with a colleague or a subject expert for further assistance in solving the equation.