arcTomato
- 104
- 27
- TL;DR
- Please teach me about the mass of Sgr A*
Hello
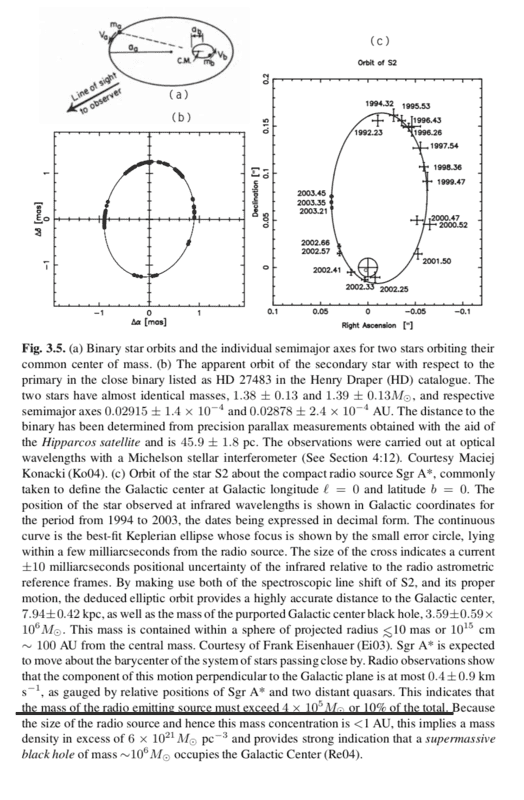
I have no idea why underline part of my pic says like that.
"Radio observations show that the component of this motion perpendicular to the Galactic plane is at most 0.4 ± 0.9 km s−1"
So What? Why this sentence shows the mass??
("The radio emitting source(underline part)" = Sgr A*?right??)
Sorry for my bad English. I'm grad if you teach me.
I have no idea why underline part of my pic says like that.
"Radio observations show that the component of this motion perpendicular to the Galactic plane is at most 0.4 ± 0.9 km s−1"
So What? Why this sentence shows the mass??
("The radio emitting source(underline part)" = Sgr A*?right??)
Sorry for my bad English. I'm grad if you teach me.