Confused about the axis of rotation in rotational motion w/o slipping

[ago01]

I'm now learning about rotational motion without slipping and it's really hurting my brain to think about. Imagine a cylinder rotating on a flat plane.

I can accept that there is both translational and rotational motion. For example, a given point on the circumference of the cylinder follows a cycloid pattern while the center of mass translates in a straight line. I can also accept that give the directions of the forces a point directly in contact with the plane has an instantaneous velocity of zero.

But in my class the axis of rotation is constantly referenced as the point in contact with the plane. This is really, really difficult for me to conceptualize. I will provide a diagram to hopefully demonstrate why I am so confused. It does not help that there wasn't a whole lot of expansion on the reason this is the axis of rotation. It was just taken as fact.

I am under the understanding the axis of rotation is the thing something rotates around. So an axis going through a cylinder's center would see the cylinder rotating much like a paper towel would when on a roller. If we put the axis on one end of the cylinder it would rotate like how the paper towel roll would rotate around the roller perpendicular to the roller.

So that would mean...

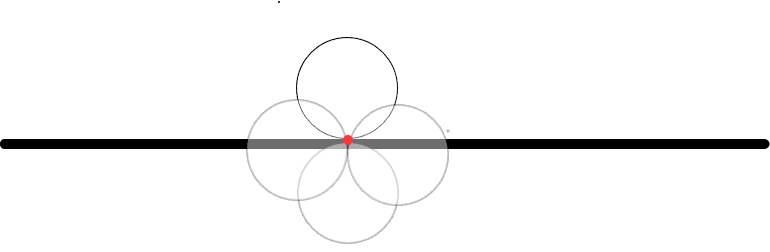
That this cross section of a cylinder should be rotating around that point. But clearly this is not the case. It's rolling forward. So I am left kind of confused. To me, it seems more natural for it to be rotating around the center of mass.

Is there a better explanation of this that could clear this up for me? I feel like I should understand this and I really don't.

 

[jbriggs444]

The idea is that one can describe the motion of the cylinder in more than one way.

One can describe it as a cylinder that is rotating clockwise around its geometric center while that geometric center is itself moving to the right. That is a nice description because it remains accurate as the cylinder keeps rolling.

Or one can describe it as a cylinder that is rotating clockwise around the point of contact of cylinder with ground while the cylinder's material at the point of contact remains stationary. This description is only valid briefly. But for the moment when it is valid, the motion of the cylinder can be completely described as a pure rotation with no translation.

In general, the "instantaneous center of rotation" is that point (or axis) on a rigid, rotating body that is momentarily stationary in one's chosen frame of reference.

 

[ago01]

Or one can describe it as a cylinder that is rotating clockwise around the point of contact of cylinder with ground while the cylinder's material at the point of contact remains stationary

I suppose this is where I am confused. The point of contact is stationary so the term around is confusing me. It's more like it's rotating on. Is this just terminology is the actual definition is arrived using your last statement:

In general, the "instantaneous center of rotation" is that point (or axis) on a rigid, rotating body that is momentarily stationary in one's chosen frame of reference.

We never really discussed this part. The examples were typical, cylinders, spheres, rings, etc all with easy to deduce "natural" axes of rotation.

 

[PeroK]

I suppose this is where I am confused. The point of contact is stationary so the term around is confusing me. It's more like it's rotating on. Is this just terminology is the actual definition is arrived using your last statement:

Let's start with a simpler example of a particle moving in a circle. At each time its instantaneous velocity is in a direction tangential to the circle. But, this velocity is only instantaneous and does not continue for any finite time. If it did, then the particle would be moving in a straight line for a time. We could draw an arrow at a point on the circle indicating the velocity at that point, but this arrow is only valid for an instant: the particle does not actually follow that arrow for any finite time interval.

In your diagram, the instantaneous motion of the cylinder is the rotation shown.

So that would mean...

View attachment 293696

This is correct. But, like the velocity tangential to the circle, this diagram shows the instantaneous motion and is not valid for any finite time interval. At each instant we have a different physical point on the cylinder in contact with the ground and now the centre of rotation.

 

[Lnewqban]

A portion of your diagram would be good for a wheel stepping down from a sharp curb, for example.
There is a geometric reason for one point of the periphery to describe the curve it does when rolling on a flat surface.

Please, see:
https://www.physicsforums.com/insights/explaining-rolling-motion/

https://en.m.wikipedia.org/wiki/Cycloid

:)

 

[ago01]

Let's start with a simpler example of a particle moving in a circle. At each time its instantaneous velocity is in a direction tangential to the circle. But, this velocity is only instantaneous and does not continue for any finite time. If it did, then the particle would be moving in a straight line for a time. We could draw an arrow at a point on the circle indicating the velocity at that point, but this arrow is only valid for an instant: the particle does not actually follow that arrow for any finite time interval.

In your diagram, the instantaneous motion of the cylinder is the rotation shown.This is correct. But, like the velocity tangential to the circle, this diagram shows the instantaneous motion and is not valid for any finite time interval. At each instant we have a different physical point on the cylinder in contact with the ground and now the centre of rotation.

Okay so let me try this on for size. I was playing with my dog funny enough and I was thinking about what forces were being applied when I lifting him up by his chest.

So when I lift my dog from his chest his feet are still on the ground. I am apply a torque to him to cause him to rotate upwards around the fixed point at his rear paws. If I was to continue this torque eventually he would roll over onto his back around that axis of rotation (through his paws). He could also be rotating by his center of mass, but also his paws if we choose.

It seems this is the same process as the ground axis of rotation of the cylinder. Since the point of contact is instantaneously at zero all other points are instantaneously being torqued around the fixed point on the ground since they have a non-zero velocity and are some distance (the lever arm) away from the point of rotation.

If this is correct, I think I finally get it!

 

[PeroK]

I can't see the analogy with rolling motion there.

 

[ago01]

I can't see the analogy with rolling motion there.

Its that in rolling motion, the other points are being torqued around an instantaneous fixed point on the ground. Maybe its easier to see what I am getting at with a simpler shape (unlike dogs).

If we take a rod and set the axis of rotation at one end of it perpendicular to the side, when you apply a torque to this rod it will rotate around that axis (the point where it touches, really). That point is fixed - it doesn't move.

So if the analogy changes a little, the axis of rotation in the cylinder is the ground. Just like a point at the other end of the rod previously, a point on the cylinder has a torque applied to it that causes it to rotate around that fixed point (instantaneously). As a previous poster said this is only true in the instant, as in the next instant the new fixed point at the axis of rotation will have changed to a different point on the surface of the cylinder. But for that instant all other points on the cylinder are rotating around that fixed point on the ground by virtue of them experiencing a torque.

 

[PeroK]

If a cylinder is rolling without slipping at constant velocity, then there is no torque. Angular momentum is conserved.

 

[jbriggs444]

Its that in rolling motion, the other points are being torqued around an instantaneous fixed point on the ground.

The points are moving in arcs under a center-directed acceleration regardless of whether we choose to reference the cylinder's motion around a "moving" axis at the center of mass or around a "stationary" axis on the ground.

My understanding of the word "torqued" would mean that the points are subject to a torque which twists them into motion. Not so.

 

[ago01]

If a cylinder is rolling without slipping at constant velocity, then there is no torque. Angular momentum is conserved.

The points are moving in arcs under a center-directed acceleration regardless of whether we choose to reference the cylinder's motion against a "moving" axis at the center of mass or a "stationary" axis on the ground.

My understanding of the word "torqued" would mean that the points are subject to a torque which twists them into motion. Not so.

It is now clear to me I should not use terminology I learned a few chapters ago :P.

The arc explanation might be actually what I was getting at by using torque... I haven't learned about angular momentum yet but I see that I am wrong by saying torque. The analogy might have worked with the rod but not with the cylinder. My apologies.

So these arcs the points are rotating through due to their center directed acceleration is causing them to instantaneously rotate about the point on the ground (or the center axis) since they're moving around the cylinder while the fixed point stays still (in that instant).

This actually makes a lot of sense. I think I understand it if the above is correct and I really appreciate everyone bearing with me while I try to wrap my head around this.