schniefen
- 177
- 4
- Homework Statement
- Consider the function ##p(t)=\sin{(t/\tau)}## for ##0\leq t <2\pi \tau## and ##p(t)=0## for ##2\pi \tau \leq t < T##, which is periodically repeated outside the interval ##[0,T)## with period ##T##. Plot this function for ##\tau=T/30## using a restricted set of Fourier coefficients.
- Relevant Equations
- The complex Fourier series: ##\sum_{j=-\infty}^{\infty} a_j e^{i2\pi jt/T}##. Since the ##p(t)## is real-valued, we have ##a_{-j}=\overline{a_j}##.
I have plotted the function for ##T=15## and ##\tau=T/30## below with the following code in Python:
Output:
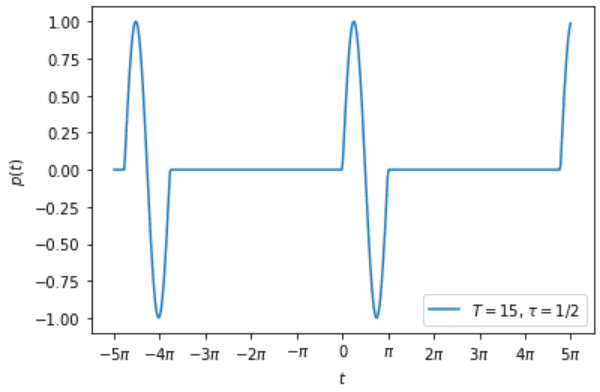
I would now like to plot an approximation to this function using a restricted set of Fourier coefficients. How can I do that in python?
Code:
import numpy as np
import matplotlib.pyplot as plt
def p(t,T,tau):
n=np.floor(t/T)
t=t-n*T
if t<(2*np.pi*tau):
p=np.sin(t/tau)
else:
p=0
return p
tdata=np.linspace(-5*np.pi,5*np.pi,500)
pdata=[]
for i in tdata:
pdata.append(p(i,15,1/2))
plt.plot(tdata,np.array(pdata),label='$T=15$, $\u03C4=1/2$')
plt.legend(loc='lower right')
tick_pos= [-5*np.pi,-4*np.pi,-3*np.pi, -2*np.pi , -np.pi, 0, np.pi , 2*np.pi,3*np.pi,4*np.pi,5*np.pi]
labels = ['$-5\pi$','$-4\pi$','$-3\pi$','$-2\pi$','$-\pi$','0', '$\pi$', '$2\pi$','$3\pi$','$4\pi$','$5\pi$']
plt.xticks(tick_pos, labels)
plt.xlabel('$t$')
plt.ylabel('$p(t)$');Output:
I would now like to plot an approximation to this function using a restricted set of Fourier coefficients. How can I do that in python?