Homework Help Overview
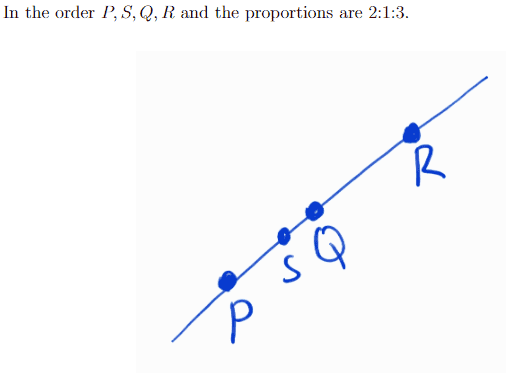
The discussion revolves around plotting points in three-dimensional space, specifically focusing on the coordinates of four points: P(8,2,6), R(-2,16,-2), Q(3.9,2), and S(14/3, 20/3, 10/3). Participants are exploring the implications of a given proportion (2:1:3) in relation to these points.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning
Approaches and Questions Raised
- Participants are questioning the meaning of the proportion 2:1:3 and how it relates to the points. There is discussion about plotting the points in 3D space and the necessity of visual representation for understanding their arrangement. Some participants suggest using distance calculations between vectors to determine relationships among the points.
Discussion Status
The conversation is ongoing, with participants sharing insights about plotting techniques and the relevance of distance calculations. Some have proposed alternative methods, such as using 2D projections, while others are still considering the implications of the 3D representation.
Contextual Notes
There are mentions of potential confusion regarding the ordering of points without visual aids, as well as varying approaches to simplifying calculations, such as scaling coordinates. Participants are also reflecting on the adequacy of different dimensional representations for solving the problem.
 ,
,