Shape of y = 3x +2 in r - \theta space

[Mark44]

In the third plot, it's really plotting the equation $y = \frac 2 {\sin(x) - 3\cos(x)}$, but with the axes labeled as r (for y) and $\theta$ (for x). I don't know what you did in the fourth graph.

 

[OmCheeto]

...I don't know what you did in the fourth graph.

It's x plotted as r, and y plotted as $\theta$, on a polar graph.

 

[Mark44]

It's x plotted as r, and y plotted as $\theta$, on a polar graph.

What was the equation you plotted? This doesn't look like the polar graph of $r = 3\theta + 2$. That graph would be a spiral.

 

[BvU]

This looks like plotting cats on the orange line, and dogs on the apples line

It's just naming things. However, I only see black and blue
But for a plot of the $r-\theta$ plane (the solution to exercise 1.14!) concentrate on $[0,2\pi)$ in the first quadrant.

But you knew that.

Can't make sense of the fourth plot either:

It's x plotted as r, and y plotted as $\theta$, on a polar graph

expect only one x=0 and one y=0

 

[OmCheeto]

What was the equation you plotted? This doesn't look like the polar graph of $r = 3\theta + 2$. That graph would be a spiral.

Can't remember now.
hmmm...

x = π/2 * cos(θ)
y = π/2 * sin(θ)
from θ between -π to +π
plotted on a polar graph

This looks like the plot from exercise 1.13, where r is a constant.

 

[BvU]

Making a mess of things eh ?
Bedtime 4me

 

[Ray Vickson]

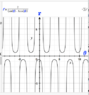
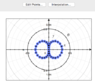
Because Pushoam used the Mathematica Plot function. This function plots an equation using Cartesian coordinates. In this case it merely relabels y as r, and x as $\theta$, exactly as @OmCheeto said.

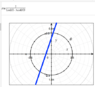
Especially as we don't see what the author means by "r - $\theta$ space" in the few pages of the linked-to textbook that we have access to. "r - $\theta$ space" is not standard mathematical terminology, in my experience. If the author of this book has not stated what he means by this terminology, that's a very sloppy oversight.In an actual polar coordinate system, if r is fixed and $\theta$ is allowed to vary, you can an arc along a circle. In this so-called "$r - \theta$ space," where r and $\theta$ are merely aliases for x and y, then yes, you would get a straight line segment, one that is horizontal.

The whole exercise seems very flaky to me, and seems to boil down to this:
1. Start with the equation y = 3x + 2.
2. Convert to polar form: $r\sin(\theta) = 3r\cos(\theta) + 2$
3. Solve for r: $r = \frac 2 {\sin(\theta) - 3\cos(\theta)}$
4. Rename r to y and $\theta$ to x
5. Plot the resulting equation: $y = \frac 2 {\sin(x) - 3\cos(x)}$
Perhaps the author has a point in doing this, but without seeing more of the book than the few pages we have access to, it's not clear to me why we are doing this silly exercise.

I think this is what the author has in mind (at least, as I see it), but I think also he/she wants proper limits on $\theta.$

If you look at points $(x,y)$ on the line, then you need to look at what happens to $\theta$ as $(x,y)$ scoots along the line to $(\infty, \infty)$ in the northeasterly direction, and what happens to $\theta$ as $(x,y)$ scoots along the line to $(-\infty, -\infty)$ in the southwesterly direction.

A valid plot of the line in $(r,\theta)$ space must have $\theta$ lying between those two extreme values.

 

[LCKurtz]

I'm a bit late to this thread but... I don't see any notational difference between the assigned exercise and a typical change of variable problem like: given the square given by $$x+y=1,~x+y=-1,~-x + y = 1,~-x+y=-1$$which could as well be written as $|x|+|y|=1$,
and the change of variables $u=x+y,~v = -x+y$, what does the graph look like in $u,v$ space? So I'm agreeing that the solution in post #16 is correct. It's just that for a polar coordinate change of variable we don't normally look at the geometry in that way, and I don't personally think the problem is helpful given that fact.

 

[OmCheeto]

I have his email address. I could ask him.

Sure, let's find out.

Hi [Om],

Thanks for your email...I never expected to ignite a firestorm when I wrote that exercise. I just meant for students to appreciate that in changing coordinate systems, "Straight lines may become curves and angles and distances may change...[but]...a point is still a point and a curve is still a curve."

The solution is obtained by writing x=r cos θ and y=r sin θ and obtaining r as a function of θ . I obtained r = 2/(sin (theta) - 3 cos(theta) )​

[Author]​

Good enough for me!

 

[Mark44]

Hi [Om],

Thanks for your email...I never expected to ignite a firestorm when I wrote that exercise. I just meant for students to appreciate that in changing coordinate systems, "Straight lines may become curves and angles and distances may change...[but]...a point is still a point and a curve is still a curve."

The solution is obtained by writing x=r cos θ and y=r sin θ and obtaining r as a function of θ . I obtained r = 2/(sin (theta) - 3 cos(theta) )​

[Author]​

Good enough for me!

It's just that for a polar coordinate change of variable we don't normally look at the geometry in that way, and I don't personally think the problem is helpful given that fact.

Pretty much the objection I wrote earlier in this thread. With a change of variables similar to what LCKurtz described, you have a new coordinate system and new axes. Changing to polar coordinates, though, you don't have new axes, as there is no "r axis" and no "$\theta$ axis."

Having said that, it is useful in plotting a polar curve $r = f(\theta)$ to pretend that you're graphing y = f(x). The x intercepts indicate when r on the polar graph returns to the pole, and the interval between intercepts can tell you the interval for $\theta$ on which r > 0 or when r < 0>.

 

[Pushoam]

Hi [Om],

Thanks for your email...I never expected to ignite a firestorm when I wrote that exercise. I just meant for students to appreciate that in changing coordinate systems, "Straight lines may become curves and angles and distances may change...[but]...a point is still a point and a curve is still a curve."

The solution is obtained by writing x=r cos θ and y=r sin θ and obtaining r as a function of θ . I obtained r = 2/(sin (theta) - 3 cos(theta) )​

[Author]​

Good enough for me!

What I understood:
Plot of y = 3x + 2 in Cartesian coordinate system ⇒ straight line ...(1)

Converting y = 3x +2 in polar form, i.e. r = $\frac 2 { \sin {\theta} - 3 \cos {\theta}}$ and plotting this in Cartesian coordinate system (or should I call it Cartesian coordinate space?) by labeling y as r and x as $\theta$, we get a curved line. I think this is what the author meant to show. ...(2)

plotting r = $\frac 2 { \sin {\theta} - 3 \cos {\theta}}$ in polar space gives a straight line. ...(3)

Learning of this thread:
If I plot an equation expressed in coordiantes of different coordinates system in the same coordinates system, then the plot of the equation expressed in different co-ordinates can have different shapes as shown by (1) and (2).

If I plot an equation expressed in co-ordiantes of different coordinates system in the corresponding coordinates system, then the plots will have same shape as shown by (1) and (3).

I think the above statements need some better rephrasing. Could anyone please do that (or tell me how to phrase well as phrasing an idea well is a skill and I need to learn it.)?