- #1
Pushoam
- 962
- 51
Homework Statement
Homework Equations
The Attempt at a Solution
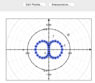
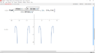
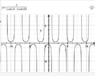
Substituting x = ## r \cos{ \theta } ## and y = ## r \sin \theta ## into the equation y = 3x +2,
I got r = ## \frac { -3 \cos{\theta} \pm \sqrt{ 4 – 31 ( \cos{\theta} )^2 } } { 10 ( \cos{\theta} ) ^2 – 1} ##Plotting it in Mathematica,




 .
.