Points on a rigid body always have the same angular speed?

[Happiness]

Consider a circle rotating about a point X on its circumference at $\omega = 2$ rad/s. That means all points on and in the circle rotate at the same $\omega = 2$ rad/s.

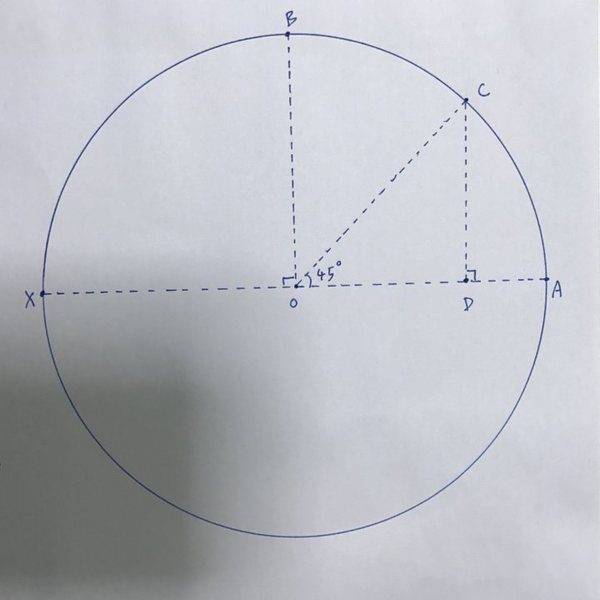
What are the angular velocities of various different points, say points A, B and C, with respect to the centre O of the circle? At first thought, different points with the same $\omega$ with respect to point X should probably have different $\omega$'s (from one another) with respect to a different point O, because if those points are rotating in sync about point X, they may not necessarily be rotating in sync about point O. But to my surprise, they do have the same $\omega$ and worse, their $\omega$ is still $2$ rad/s!

Why so? Any mathematical proof or intuitive explanations?

Some notes on my calculations:
To calculate the $\omega$ of a point A relative to point O, I take the velocity of A relative to that of O divided by the distance between A and O.
I also calculated the $\omega$'s of points A, B and C relative to point D. They are equal to $2$ rad/s too!

 

[Comeback City]

I also calculated the w's of points A, B and C relative to point D. They are equal to 2 rad/s too!

And that isn't a coincidence.

I guess it may seem counterintuitive because anglular velocity doesn't behave the same as linear velocity. Distance from point of rotation must be taken into account in angular, as you noted.

 

[zwierz]

Angular velocity is a characteristic of rigid body's motion. It does not make sense to speak about angular velocity of an individual point of the rigid body

 

[A.T.]

It does not make sense to speak about angular velocity of an individual point of the rigid body

You can define the angular velocity of any point relative to some other point:
https://en.wikipedia.org/wiki/Angular_velocity#Angular_velocity_of_a_particle

 

[PeroK]

Why so? Any mathematical proof or intuitive explanations?

https://www.physicsforums.com/threa...-rotation-other-than-com.896718/#post-5642572

 

[zwierz]

ou can define the angular velocity of any point relative to some other point:

No you cannot. Because a trajectory of the point can be essentially spatial curve. By the same reason your definition does almost nothing with angular velocity of the rigid body.

UPD

 

[A.T.]

... your definition does almost nothing with angular velocity of the rigid body.

Yes, this general definition for a point is different from the definition for a rigid body.