Polar Graphs and a question about their poles

[m3dicat3d]

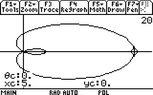
Trying to help someone out with their assignments on basic polar graphs. This first question is very easy to determine the poles from as the limacon has an inner loop.

View attachment 829

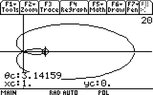
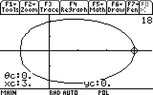
But when you have a limacon WITHOUT (below) an inner loop, how does the "max from pole" and "min from pole" figure? It's been years since I've done this, but my gut is saying it has simply one pole, and the "max" and "min" are the same. For example:

View attachment 830

So in the case of the above problem, wouldn't bot "max" and "min be 4?

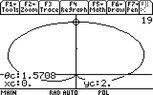
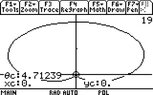
And if this is case, would you handle a cardioid the same way, for instance:

View attachment 831
Would this have both "max" and "min" as 2?

Thanks again :)

 

[I like Serena]

Hi m3dicat3d! :)

The pole is simply the origin.
See for instance wiki about the Polar coordinate system:

The fixed point (analogous to the origin of a Cartesian system) is called the pole, and the ray from the pole in the fixed direction is the polar axis. The distance from the pole is called the radial coordinate or radius, and the angle is the angular coordinate, polar angle, or azimuth.​

The max from pole and min from pole are the maximum and minimum values for r.

 

[m3dicat3d]

Thanks so much!

Let me try to clarify here so I'm not explaining this to the person I'm trying to help incorrectly.

Since the pole is analogous to the origin of a Cartesian system, we are finding the max and min values of r from the pole for the given function. In the case of a cosine function, considering that cosine has its max and min values at 0 radians and pi radians respectively, we would evaluate any of the three given equations at 0 and pi to determine max and min for cosine polar graphs.

Similarly, for sine polar graphs, we would evaluate max and mins at pi/2 and 3pi/2.

View attachment 835View attachment 833View attachment 834

So for the polar equation given above, the max at 0pi is 5 and the min at pi is 1.View attachment 836View attachment 837View attachment 838

Likewise our max is 3 and min is 1 here...

View attachment 842View attachment 840View attachment 841

And for the above Cardiod, the max is 2 (evaluated at pi/2) and the min is 0 (evaluated at 3pi/2)Am I understanding this better now?

P.S. Sorry about the attached thumbnail below, don't know how I managed that :p

 

[Petrus]

View attachment 835View attachment 833View attachment 834

So for the polar equation given above, the max at 0pi is 5 and the min at pi is 1.

Hello m3dicat3d,
you got a typo there :) it should be min is $$-1$$:)
edit: Should you not answer if it is a loop or no loop and $$\frac{\pi}{2}$$ intercept as well?

Regards,
$$|\pi\rangle$$

 

[m3dicat3d]

Thanks Petrus!

Sounds as if I'm on the right track here. Yes, the intercept and loop questions we are working through, I just didn't include them here as I understand what we needed to do with those, and just focused on what I was unsure of.

View attachment 843View attachment 844View attachment 845

As far as the min @ -1 typo, were you referring to the no loop limacon above? If you meant the cardioid then I may be missing something else. Thanks :)