Possible equation for this graph?

  • Context: Undergrad 
  • Thread starter Thread starter rjmchung
  • Start date Start date
  • Tags Tags
    Graph
Click For Summary
SUMMARY

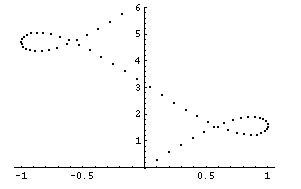
The discussion centers on deriving a parametric equation for a specific graph using the function g(n). The equation is defined as g(n) = sin(n*pi/31)*(i hat) + (sin(2*pi*n/31)+n/10)*(j hat). This formulation incorporates trigonometric functions and linear components to describe the graph's behavior across the horizontal and vertical axes, represented by (i hat) and (j hat), respectively.

PREREQUISITES
  • Understanding of parametric equations
  • Familiarity with trigonometric functions
  • Basic knowledge of graphing in a Cartesian coordinate system
  • Experience with mathematical notation and vector representation
NEXT STEPS
  • Explore the properties of parametric equations in detail
  • Study the behavior of sine functions in graphing
  • Learn about vector representation in two-dimensional space
  • Investigate the implications of adding linear components to trigonometric functions
USEFUL FOR

Mathematicians, physics students, and anyone interested in graph theory and parametric equations will benefit from this discussion.

rjmchung
Messages
1
Reaction score
0
What could be the equation (probably parametric) for this graph?

Screen Shot 2012-01-22 at 12.21.43 PM.png
 
Mathematics news on Phys.org
Let the horizontal axis be denoted by (i hat) and the vertical axis be (j hat) and call the function g(n). The function would be something like:

g(n) = sin(n*pi/31)*(i hat) + (sin(2*pi*n/31)+n/10)*(j hat)
 

Similar threads

Undergrad Adding 'z' to 2D graph equation
  • · Replies 3 ·
Replies
3
Views
2K
MHB 7.t.27 write eq for a sinusiol graph
  • · Replies 2 ·
Replies
2
Views
1K
High School Looking for free graphing calculator for two-variable inequality
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Find Smallest Subtree of G w/ Nodes from S
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Traffic simulation : directed graph including specific rules
  • · Replies 5 ·
Replies
5
Views
2K
High School Just for fun: Cubic Graph Plot
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad The number of intersection graphs of ##n## convex sets in the plane
  • · Replies 2 ·
Replies
2
Views
1K
High School What Math Class Teaches us how to Draw a Graph?
  • · Replies 23 ·
Replies
23
Views
3K
Undergrad Equation to graph a sine wave that acts like a point on a unit circle
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Finding if a subgraph of a minimal non-planar graph is maximal planar
  • · Replies 1 ·
Replies
1
Views
2K