Find Smallest Subtree of G w/ Nodes from S

[Sneaky6666]

I have a unique problem and looking for a known fast algorithm for it. I have an unweighted but directed graph `G`. I then have a subset collection of nodes `S` existing in `G`. I want to find the minimum sub tree in `G` such that it contains all the nodes in `S`.

I so far found Chu-Liu/Edmonds algorithm but it is for finding the MST for all nodes in the graph.

Does anyone know how to do this for a subset of nodes?

Example

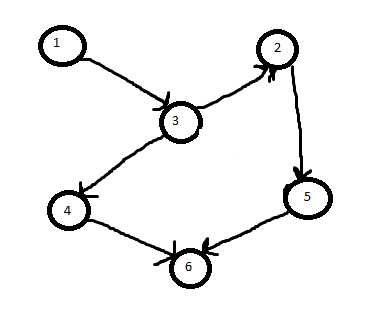
If the picture is G. And S is the node set {1, 6}. Then the solution (smallest sub tree) is the subset graph of {1, 3, 4, 6} since it includes the nodes of S. It wouldn't be {1, 3, 2, 5, 6} (even though it includes the nodes of S) because that is larger.

Thanks

 

[.Scott]

The ideal solution to this would be very similar to the traveling salesman problem - which is NP complete.
I very much suspect this is also NP complete.

My exact attack on this problem would depend very much on other specifics such as:
Is only an ideal solution good enough?
What is the cost of non-ideal solutions?
What is the range of node set sizes you will be working with?
What kind of processor power is available and how quickly do you need an answer?

 

[Filip Larsen]

I am not familiar with Chu-Liu/Edmonds, but if you start with the nodes M=S is it then not enough to "simply" find shortest path (Dijkstra's algorithm) between each node in M that ends with a different node in M (possibly handling cycles if S is not a tree) and then add those to M?

1 min later: well, I guess its possible to make an S that such that the set M as constructed above will not be the minimal solution. Right, disregard my question please.

 

[Sneaky6666]

I was thinking about this, and what I had in mind is first we pick a random node in S, and do a BFS traversal from that node, basically storing 2 pieces of data in every node. First is the smallest distance from the current node to the starting node, and a reference of the previous node to the current node (for the shortest distance path).
So while doing the BFS, if it checks a node and sees the distance for it is smaller than a previous calculated distance, then it overwrites the data stored on that node with the better one.

In the end, every node knows its shortest distance, and a reference to the previous node, which allows a path to form from the current node to the starting node. If we take all the paths and combine them, we can construct a sub tree.

What do you all think of this?

 

[Sneaky6666]

The ideal solution to this would be very similar to the traveling salesman problem - which is NP complete.
I very much suspect this is also NP complete.

My exact attack on this problem would depend very much on other specifics such as:
Is only an ideal solution good enough?
What is the cost of non-ideal solutions?
What is the range of node set sizes you will be working with?
What kind of processor power is available and how quickly do you need an answer?

I think only ideal, exact solutions are enough. Range of S, could be anything, from 1 node to all nodes in G. We can take our time doing any calculations, even if its 5 seconds and have a very strong processor.

 

[.Scott]

I would start by identifying all "unavoidable" paths - the ones that, if eliminated, would result in some of the target nodes being isolated from the home node.
Then, each of those unavoidable paths becomes a separate problem (think recursion) and all the target nodes from that unavoidable path can be treated in the parent problem as a single "target node".

Once you are left with a problem (either the original problem or a child problem from the recursion) with no "unavoidable paths", then you need to attempt to find "independent" target nodes or groups of target nodes, node groups which cannot share a path home with any node outside of the group. Those independent groups can be identified by listing all node path segments then following all paths home for each target node (think tree search) and adding the target node id to the list of nodes for each path segment used by that node. So for every node path segment (the line between adjacent nodes), you have a list of target nodes that might find that path segment useful. Then, starting at the home position, work out through the network and look for nodes that have down-tree path segments (DTPSs) (or sets of DTPSs ) with no target node overlaps. The most straight forward way of finding such groups is brute force. If there are 7 DTPSs, go through values 1 to 126 expressed in binary - each of the 7 bits representing whether the corresponding DTPS is part of candidate group 0 or candidate group 1. Then tally the target node coverage for each DTPS group - if there is clean split of the target nodes, then they are independent and can be treated as separate problems (recursion). Once a group split has occurred, each of the two smaller groups should also be tested to see if there aren't three or more independent DTPS groups.

That DTSP group processing can be done in concert with the "unavoidable path" checking. Depending of the characteristics of you problem set, identifying the "unavoidable" before the "independents" may be more or less optimal.

Once you have a problem with no "unavoidables" or "independents", you're probably at the NP point. The most brute force method would simply be to do elimination trials. Pick a path to eliminate then attempt to solve the problem without it. Since all "unavoidables" have already been sidelined, at least one solution will be found. Note its score, restore it, and disable the next one. This scoring process will also be implemented recursively. It will be be similar to tree search where you are looking for the best score.

So this will give you only ideal solutions.
Since you have placed no size limits on S or G and no topology limits on G, there is no guarentee that your "strong processor" will complete this task within 5 minutes or 5 centuries.