Potential Difference Between Capacitors in Circut

[nolachrymose]

Homework Statement

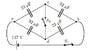
The capacitors in the figure are initially uncharged and are connected as in the diagram (attached). Then switch S1 closed and switch S2 is left open.
After a long wait, what is the magnitude of the potential difference V_{cd}? Answer in units of V.

Homework Equations

C = \frac{Q}{\Delta V}
Effective Capacitance of Capactors in Series: \frac{1}{C_{eq}} = \frac{1}{C_{1}} + \frac{1}{C_{2}}
Effective Capacitance of Capacitors in ||: C_{eq} = C_{1} + C_{2}

The Attempt at a Solution

From the diagram, we can see that the two capacitors on top and the two on both are each in series. Therefore, using the formula for capacitors in series, the effective capacitance of the two top is 1.84e-5, and the same for the two on the bottom.

The top and bottom capacitors then form a || series, so we can add their capacitances to determine the total effective capacitance of the circuit = 3.68e-5.

We know that the voltage of the battery is 137V and we know the effective capacitance of the circuit, therefore we can calculate that Q = C/\V = 0.0050416 C.

We can then use the formula C = \frac{Q}{\Delta V} to calculate the potential at c and d. C is at the end of a 92 microF capacitor, so using the formula, /\V = 54.8V. D is at the end of a 23 microF cap., so /\V = 219.2V. Therefore, V_{cd} = V_{d} - V_{c} = 219.2 - 54.8 = 164.4V. However, this answer is wrong.

I'm not sure where I went wrong in this problem. I believe I solved the effective cap. of the circuit correctly, but maybe my calculations for the potential at c and d were erroneous. Any direction in solving this problem would be really appreciated. Thanks!

 

[gneill]

You have two separate voltage dividers: the two top capacitors form one, and the two bottom capacitors form another. How does voltage distribute across series capacitors?

 

[nolachrymose]

In series capacitors, the sum of all voltages in the capacitors equals the voltage of the battery. But how does that help me solve the problem?

Since the top two capacitors are effectively equal to those of the bottom two, the voltage of the battery should be split half and half, making the voltages equal. Therefore, the potential difference would be 0, which is incorrect.

What am I missing?

 

[gneill]

Yes, the sum of the voltages for two series capacitors does equal the total voltage across the individual capacitors. The question is, how does the voltage split between the two series capacitors?

 

[nolachrymose]

Oh, I just figured it out! Because the capacitors on top and bottom are parallel, their charges must add. Since the total capacitance of each is the same, the charge on each must be equal to Q/2, not Q. Therefore, the potential difference must be half of what I'd originally found.

However, I'm having trouble finding the answer to the next part. It states: "After closing switch S_{2}, what is the potential difference V_{ad}."

The potential at a should be 0 because of the orientation of the battery. The capacitance at d, as found in the previous part, is 109.6. Therefore, the potential difference should be 109.6 - 0, but that's not correct.

I'm still not sure what I'm missing? And I was wondering if there was a good resource out there online that might help me better understand this material as a whole, because I'm struggling?

 

[gneill]

The capacitors on top and bottom are not in parallel. Each shares only one lead in common.

Tell you what. Cover up the two bottom capacitors and pretend that they don't exist. You're left with two capacitors in series, connected to a 137V battery. What is the voltage across each of the capacitors individually?