SUMMARY
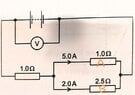
The discussion centers on the concept of potential difference in electrical circuits, emphasizing that in idealized scenarios, a wire is considered 'perfect'. This means that the potential at any point along the wire is uniform, ensuring that connected components, such as resistors A and B, maintain the same potential. This principle is crucial for solving basic electrical problems accurately.
PREREQUISITES
- Understanding of basic electrical concepts, including voltage and potential difference.
- Familiarity with Ohm's Law and its applications.
- Knowledge of circuit components, specifically resistors.
- Basic grasp of electrical circuit theory and ideal conditions.
NEXT STEPS
- Study the concept of 'ideal wires' in electrical engineering.
- Learn about the implications of potential difference in series and parallel circuits.
- Explore the effects of resistance on potential difference using Ohm's Law.
- Investigate real-world applications of electrical circuit theory in engineering.
USEFUL FOR
Students studying electrical engineering, educators teaching circuit theory, and anyone interested in understanding the principles of potential difference in electrical circuits.