Potential energy harmonic oscillator

[HWGXX7]

Hello,

I have this problem with deriving the formule from de definition of potential energy

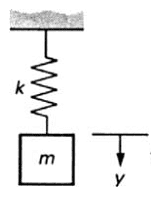
Picture show a mass-spring system in rest position:

In general potential energy can be written as dot product: \frac{dE_{P}}{d\overrightarrow{y}}=-\overrightarrow{F}.

Potential energy wil rise if, y rises. Because the direction of F is always inverse of y, this is correct.

But when the mass wil move upward trough it's equilibrium the potential energy will also rises, while y will decline. The derivative is negative, so the formule potential energy doesn't count anaymore.


How to fix this problem?

Also if you can look to my derivation of potential energy:

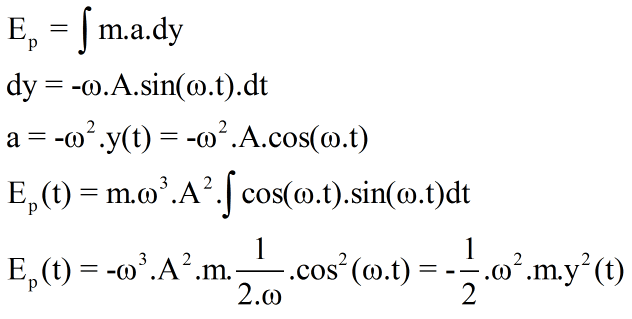
ty&grtz

 

[haruspex]

I don't see a problem. When y goes negative F will be positive, so -F is negative. That's consistent with the derivative being negative, as required.

 

[HWGXX7]

When y goes negative F will be positive, so -F is negative. That's consistent with the derivative being negative, as required.

Yes, I must have missed this

But in my derivation I get a negative result...How fix this?

ty&grtz

 

[haruspex]

You're puzzled that you get a negative potential energy?

You wrote correctly that
dEp/dy=−F
But in the very first line of your derivation you lost the - sign, making it
Ep = ∫m.a.dy
where F = m.a

 

[HWGXX7]

There is difference between: -dF.dy=dE_{p}and -d\overrightarrow{F}.d\overrightarrow{y}=dE_{p}

Second thing is a dot product, force vector opposes the direction of the position vector. So I get: -d\overrightarrow{F}.d\overrightarrow{y}=-dF.dy.cos(\theta)

The angle bewteen those is \pi, so I get: -d\overrightarrow{F}.d\overrightarrow{y}=dF.dy

Therefore: E_{p}=\int m.a.dy
and the potential energy will be negative. My question: how do I have to interprete this minus sign? Is this because of the sign convection in my dot product, are do I (may I) have to interprete the potential energy as an absolute value...

ty

 

[haruspex]

force vector opposes the direction of the position vector. So I get: -d\overrightarrow{F}.d\overrightarrow{y}=-dF.dy.cos(\theta)

ty

Even in scalars, it helps to be consistent about the positive and negative directions.
By saying that the angle between the F and dy vectors is pi, you are effectively choosing to measure F and y in opposite directions. As a consequence, you have a and y in opposite directions, so you end up with the wrong sign on Ep.
Better to say the angle between the vectors is zero, and an upward F (in the diagram) will have a negative value.

 

[HWGXX7]

The mass is moving downwards to the position where its potential energy is maximum. Potential energy will rise becasue of:
\frac{d\overrightarrow{E_{p}}}{d\overrightarrow{y}}=-d\overrightarrow{F}

The dot product d\overrightarrow{F}.d\overrightarrow{y} is negative because force vector ans position vector opposes...

Can I use this interpretation to derive the potential energy as function of position y(t)?
If not: what do I have to change in the assumptions and why ?

ty&grtz

 

[haruspex]

I have no problem with your vector equation (except that lately you've taken to writing dF where you mean F). I will use italics for vectors - it's easier.
So -F.dy will be positive, as required.

The mistake you made was in converting to scalar form. Strictly it becomes
dE = -|F||dy|cos(θ) (1)
but this is awkward because as the object oscillates θ will flip between π and 0.
To get around that, choose as convention that scalars F and y are measured in specific directions. They don't have to be the same direction, but if they're not you're likely to get confused, so let's take downwards as positive for both.
When θ = π, F and dy have opposite sign, so F.dy = -|F|.|dy| = |F|.|dy|.cos(θ).
When θ = 0, F and dy have the same sign, so F.dy = +|F|.|dy| = |F|.|dy|.cos(θ).
So either way, F.dy = |F|.|dy|.cos(θ).
Substituting in (1) we get
dE = -F.dy

(I think the lesson here is not to start in vectors for a problem which can easily be managed with scalars!)

 

[HWGXX7]

Oké, think I got it. Thank you for the help!

grtz