FrankJ777
- 140
- 6
Hi guys. I have some questions about the practical use of a quarter wave transformer to match loads. For my question please refer to the figure below...
According to my reading the input inpedance fo a quarter wave transformer is:
Zin = Z12/ZL
and to properly match the line with characteristic impedance Z0 to the load ZL, Z1 must be chosen so that:
Z1 = √Z0ZL
So it seems that for the quarter wave transformer to be useful I wave to be able to choose a transmission line of the appropriate impedance Z1. When would that be of practical use? If i have only coax of 50Ω or75Ω etc., it seems I would have a difficult time finding an instance where I could use a quarter wave transformer. Obviously I'm missing something.
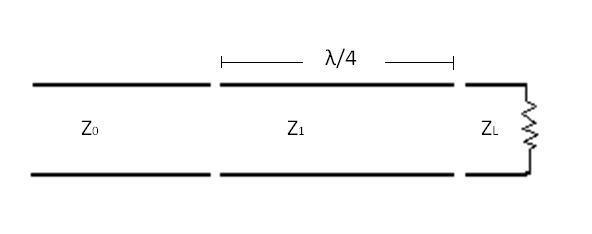
According to my reading the input inpedance fo a quarter wave transformer is:
Zin = Z12/ZL
and to properly match the line with characteristic impedance Z0 to the load ZL, Z1 must be chosen so that:
Z1 = √Z0ZL
So it seems that for the quarter wave transformer to be useful I wave to be able to choose a transmission line of the appropriate impedance Z1. When would that be of practical use? If i have only coax of 50Ω or75Ω etc., it seems I would have a difficult time finding an instance where I could use a quarter wave transformer. Obviously I'm missing something.