Precession of angular momentum in vector model

[Jan Hidding]

Hey everyone,
I just made an account because I have a problem concerning angular momentum and precession.

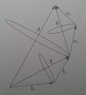
In the picture below you see the vectors l1 and l2 that make up total orbital angular momentum L precess around L. I can get my head around why that is the case. The same for s1 and s2 around S and L and S around J.

Precession and angular momentum have always been a weak subject for me, so if you could try to explain it as easy as possible that would be great :).

Thanks in advance!

 

[DrClaude]

Lets start by considering a single vector which corresponds to a eigenstate of $\hat{L}^2$ and $\hat{L}_z$, $| l,l \rangle$ (i.e., $m = l$). Since $\hat{L}^2 | l,l \rangle = l(l+1) \hbar^2 | l,l \rangle$, the classical vector has length $\sqrt{l(l+1)}$, with a projection on the z axis given by $\hat{L}_z | l,l \rangle = l \hbar | l,l \rangle$. This means that the vector does not point exactly along the z axis, but is at a slight angle. Because $\hat{L}_x$ and $\hat{L}_y$ do not commute with $\hat{L}_z$, this means that the projection of the vector on the xy plane is undefined. Classically, this is represented either by drawing the cone resulting from the rotation of the vector around the z axis ("cone of uncertainty"), or by considering that the vector is precessing around the z axis.

This is of course a classical representation of something quantum mechanical, but it is a good picture to represent the uncertainty due to the non-commutation.

When you add $l_1$ and $l_2$ into $L$, it simply displaces this uncertainty, or precession, around $L$ instead of the z axis.

 

[Jan Hidding]

Thanks for your reply. I think I understand it a bit better now. I get the fact about uncertainty of the projection on the xy-plane as they do not communte with $L^2$ and $L_z$ but how can it be that the cone is due to precession. Where does the precession of the vector comes from?

 

[maNoFchangE]

Where does the precession of the vector comes from?

The idea of precession actually becomes clearer when one considers the particle under a uniform magnetic field pointing in one direction. If the interaction between particles can be neglected, the Hamiltonian will only be due to the magnetic moment of individual particles: $H = -\frac{gq}{2m}BL_z$. For an arbitrary state $|\psi\rangle$ at $t=0$, its time evolution is given by $|\psi(t)\rangle = e^{-iHt/\hbar}|\psi\rangle$. If you the calculate the expectation value of $L_x$ with respect to $|\psi(t)\rangle$:
$$
\langle L_x \rangle_{psi(t)} = \langle\psi| e^{iHt/\hbar} L_x e^{-iHt/\hbar}|\psi\rangle
$$
You should find $\langle L_x \rangle_{psi(t)} = \langle L_x \rangle_{psi(0)} \cos\omega t - \langle L_y \rangle_{psi(0)} \sin \omega t$ with $\omega = \frac{gq}{2m}B$, which suggests that the angular momentum is precessing in time.

 

[Jan Hidding]

I think I got it now. Thanks for your help :)!