Discussion Overview
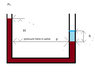
The discussion revolves around the pressure differences observed in a U-tube containing two immiscible fluids, water and oil. Participants explore the implications of fluid heights and densities on pressure readings at the same height in the tube, questioning the assumptions made in the analysis.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
- One participant questions why the pressures at the same height in the U-tube do not match, given the differing heights of water and oil.
- Another participant critiques an equation presented, suggesting it leads to absurd conclusions and indicates a misunderstanding of pressure relationships in the system.
- There is a mention of the unusual situation where a denser fluid (water) is floating on a less dense fluid (oil), raising questions about the conditions of the U-tube setup.
- Some participants seek clarification on the purpose of the attached image, wondering if it is a real scenario or a problem designed to identify mistakes.
- There is a focus on understanding the implications of pressure assumptions, particularly regarding the dashed line in the diagram and the equality of pressures on either side.
Areas of Agreement / Disagreement
Participants express differing views on the interpretation of the pressure calculations and the physical setup of the U-tube. There is no consensus on the correct understanding of the pressure relationships or the validity of the assumptions made.
Contextual Notes
Limitations include potential misunderstandings of fluid dynamics principles, the dependence on the specific conditions of the U-tube, and unresolved questions about the nature of the fluids involved.
Who May Find This Useful
This discussion may be of interest to students and educators in fluid mechanics, physics enthusiasts exploring fluid dynamics concepts, and individuals analyzing practical applications of pressure in U-tube setups.