Probability of Hypokalemia w/ 1 or Multiple Measurements

[SakuRERE]

TL;DR Summary: Finding the probability with one measurement and multiple measurements on separate days.

Question: Hypokalemia is diagnosed when blood potassium levels are low, below 3.5 mmol/L. Let’s assume we know a patient whose measured potassium levels vary daily according to N(µ = 3.8 mmol/L, σ = 0.2 mmol/L).
(a) If a single potassium measurement is made, what is the probability that the patient is diagnosed as hypokalemic?
(b) If measurements are made instead on 4 separate days, what is the probability that the patient is diagnosed with hypokalemia?

For part A -->
I solved the question as a standardized normal distribution. I tried to find P(x<=3.5),
using the standard normal formula z= X-Mean/SD I converted the X value 3.5 to a Z score and got P(x<=-1.5)
after that, I used the Gauss table to find the probability and it was P(x<=-1.5)= 0.0668
this answer was similar to the answer key provided by our professor.

However, for the second part, the answer key has to be 0.0013 but I can't think of a way to figure it out. And I don't understand how taking different measurements on separate days will influence my probability.
I will appreciate your help, thank you!

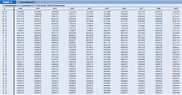
I attached the positive and negative Gauss tables for easier accessibility.

 

[Office_Shredder]

What does it even mean to be diagnosed after 4 samples? Do you have to get at least one positive? All positive?

The odds of getting more positives than negatives are
$4(.0668)^3(1-.0668)+.0668^4\approx 0.00113$ which is not that far from what the answer key says...

 

[FactChecker]

Or an average of the four below 3.5?
Some more information is needed in the problem statement.

 

[SakuRERE]

What does it even mean to be diagnosed after 4 samples? Do you have to get at least one positive? All positive?

The odds of getting more positives than negatives are
$4(.0668)^3(1-.0668)+.0668^4\approx 0.00113$ which is not that far from what the answer key says...

Thanks for replying
But I didn’t get what’s that formula you used

Thanks again

 

[Office_Shredder]

Thanks for replying
But I didn’t get what’s that formula you used

Thanks again

I added the odds of getting three positives and of getting four positives.

I have no reason to think that's what they want you to do other than the similarity of the answer.