Master1022
- 590
- 116
- Homework Statement
- Suppose that the latest Jane arrived during the first 5 classes was 30 minutes. Find the posterior predictive probability that Jane will arrive less than 30 minutes late to the next class.
- Relevant Equations
- Probability
Hi,
This is a another question from the same MIT OCW problem in my last post. Nevertheless, I will try explain the previous parts such that the question makes sense. I know I am usually supposed to make an 'attempt', but I already have the method, but just don't understand it.
Questions:
1. Where has this posterior predictive probability come from (see image for part(c) solution)? It vaguely seems like a marginalization integral to me, but am confused otherwise.
2. Why are there two separate integrals for the posterior predictive probability over the different ranges of ##x## (see image for part(c) solution, but requires a result from part (b))? Would someone be able to explain that to me please?
Context:
Part (a)

Part(a) solution:
 Part (b):
Part (b):
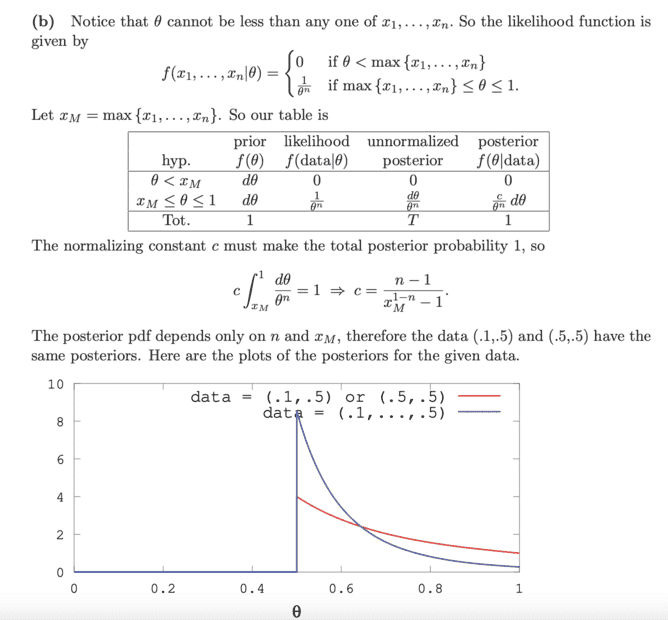
 Part (b) solution:
Part (b) solution:
Part (c):

Part (c) solution: (this is what my question is about)
 Any help is greatly appreciated
Any help is greatly appreciated
This is a another question from the same MIT OCW problem in my last post. Nevertheless, I will try explain the previous parts such that the question makes sense. I know I am usually supposed to make an 'attempt', but I already have the method, but just don't understand it.
Questions:
1. Where has this posterior predictive probability come from (see image for part(c) solution)? It vaguely seems like a marginalization integral to me, but am confused otherwise.
2. Why are there two separate integrals for the posterior predictive probability over the different ranges of ##x## (see image for part(c) solution, but requires a result from part (b))? Would someone be able to explain that to me please?
Context:
Part (a)
Part(a) solution:
Part (c):
Part (c) solution: (this is what my question is about)