Probe absorption and dressed states

[BillKet]

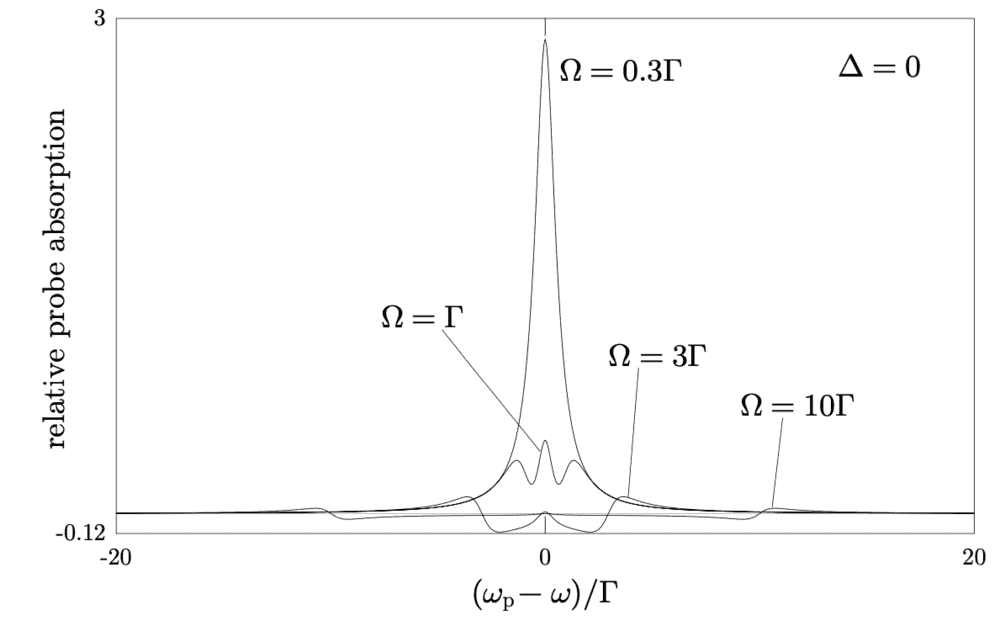
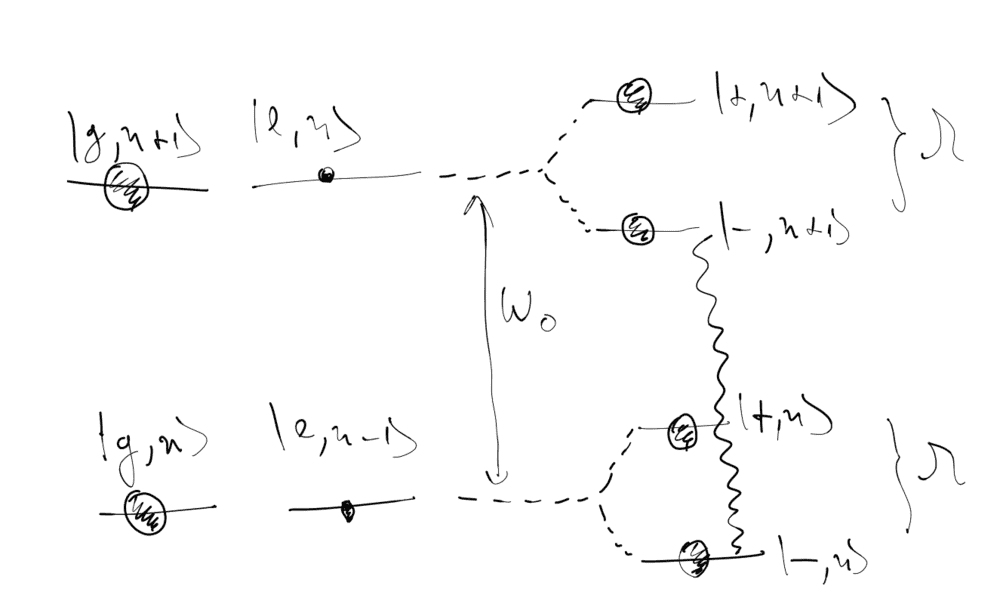
Hello! I am reading about dressed states, and I am presented a situation in which we have a laser (the pump laser) on resonance with a 2 level (atomic) transition, and a second, weak laser (probe laser) that is scanned over a frequency range. The absorption spectrum of the probe laser, for different Rabi frequencies, $\Omega$ of the pump laser is shown in the attached figure. My question here is only for the case of $\Omega = 0.3 \Gamma$. Given that we have atom laser interaction, the ground and excited state of the atom $|g>$ and $|e>$ are not eigenstates anymore. The eigenstates are, for zero detuning ($\Delta = 0$) $|+> = \frac{|g>-|e>}{\sqrt{2}}$ and $|-> = \frac{|g>+|e>}{\sqrt{2}}$. So, the actual levels that the probe laser sees are $|+>$ and $|->$. Given that the pump laser has a small power, the ground atomic state, $|g>$ will be more populated than the excited one $|e>$ (i.e. the population won't be split 50/50 as it would be for high laser power) in the steady state. However, the $|+>$ and $|->$ and equal linear combinations of $|g>$ and $|e>$, so they should have equal populations. I also attached a little drawing with the levels and populations (populations are draw as circles, with bigger circles meaning bigger population). The 2 levels connected by the wiggly line represent 2 levels that can be connected by the probe laser, assuming the probe laser is on resonance. What confuses me is: why do we get an absorption at all (according to the first figure) when the probe laser is on resonance. According to the second figure, the 2 levels connected by the probe laser (wiggly line) have equal populations (even if $|g>$ and $|e>$ have different populations)? Shouldn't the absorption be zero, given that the amount of absorption and stimulated emission would cancel each other? Can someone help me understand what am I missing here? Thank you!

 

[Twigg]

Sorry for an overly brief reply. Crazy week!

Shouldn't the absorption be zero, given that the amount of absorption and stimulated emission would cancel each other?

You have the right idea, but remember that the atom doesn't differentiate between pump laser power and probe laser power. It won't totally ignore the probe in favor of the pump. There will be competition between the two. Some of the probe will be absorbed and re-emitted, and a little bit less of the pump will be absorbed and re-emitted.

 

[BillKet]

Sorry for an overly brief reply. Crazy week!

You have the right idea, but remember that the atom doesn't differentiate between pump laser power and probe laser power. It won't totally ignore the probe in favor of the pump. There will be competition between the two. Some of the probe will be absorbed and re-emitted, and a little bit less of the pump will be absorbed and re-emitted.

Thank a lot! So basically, when the pump has low power, we need to account for the probe laser, too (i.e. we would need to solve the optical Bloch equations with 2 lasers present). If the pump has a big power (as in the case for $10 \Gamma$), the effect of the probe will be so small that we can use the dresses state picture intuition, as if the probe was not present, and this is why we actually have zero absorption on resonance for $\Omega = 10 \Gamma$.

 

[Twigg]

Yep! The effect of the probe laser on the atom population is small, but the effect of the pump on the probe spectrum is ginormous, as shown in the graph.