Problem integrating with the disk method

[Amaelle]

Homework Statement

look at the image

Relevant Equations

polar coordinates

Good day I have the following exercice and it's solved using spherical coordinates

I totally agree with the solution but I have issue to find out why mine does not work
I used the the integration by disk
I divided the region of integration to 2 A1 and A2 (A2 is the upper half sphere and A1 is the region delimitated by the cone

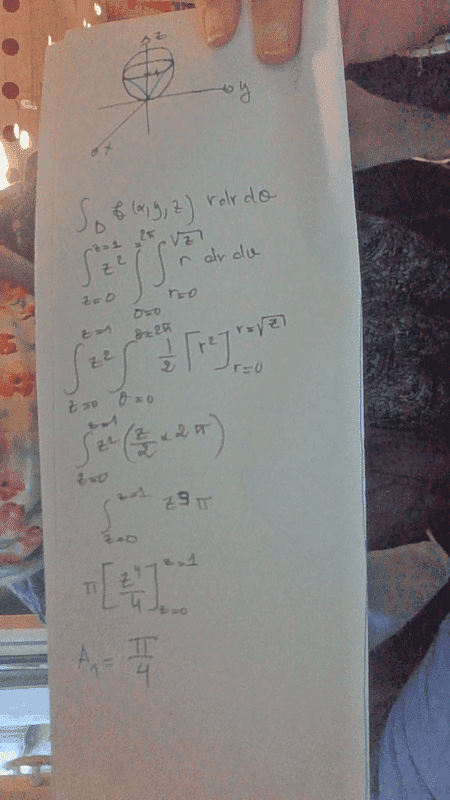
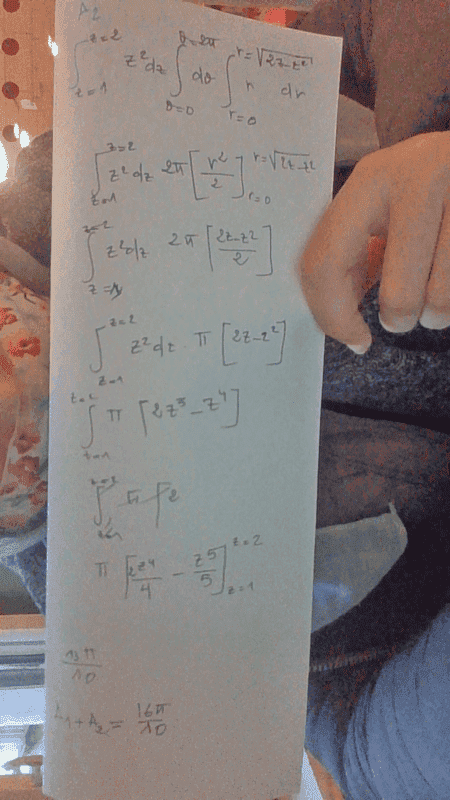Many thanks in advance!

 

[phyzguy]

How did you decide that those two regions A1 and A2 were the correct regions to plot? Try plotting r = \sqrt{x^2 + y^2} vs z for the two conditions given. What is the shape of the resulting region?

Ignore that post. I think you have the regions correct. Another question. Why did you integrate from r=0 to r=√z in the first integral. Shouldn't it be from r=0 to r=z?

Also, I think you just did the algebra wrong in the second integral. I get \frac {13 \pi}{10}

 

[Amaelle]

this is the region I'm getting
the cone region I have gotten by calculation the integral from r= 0 to r=sqrt(z)
and the half sphere region that I got from r=0 to r=sqrt(2z-z^2)
I know something is wrong here
thanks

 

[phyzguy]

Please look at the edits to my post. I agree the regions look correct, but I think you made two errors in evaluating the integrals. Correct those and see what you get.

 

[phyzguy]

Also, you should learn to input the math in latex. It is much easier for us to read than pictures of your hand-written work.

 

[Amaelle]

thanks a million! it's ok now my mistake was that r=sqrt(z)!
you saved my life!